Overview

zkMIPS is an open-source, simple, stable, and universal zero-knowledge virtual machine on MIPS32r2 instruction set architecture(ISA).

zkMIPS is the industry's first zero-knowledge proof virtual machine supporting the MIPS instruction set, developed by the ZKM team, enabling zero-knowledge proof generation for general-purpose computation. zkMIPS is fully open-source and comes equipped with a comprehensive developer toolkit and an efficient proof network. The Entangled Rollup protocol, designed specifically to utilize zkMIPS, is a native asset cross-chain circulation protocol, with typical application cases including the Metis Hybrid Rollup design and the GOAT Network Bitcoin L2.

Architectural Workflow

The workflow of zkMIPS is as follows:

• Frontend Compilation

  Source code (Rust) → MIPS assembly → Optimized MIPS instructions for algebraic representation.

• Arithmetization

  Emulates MIPS instructions while generating execution traces with embedded constraints (ALU, memory consistency, range checks, etc.) and treating columns of execution traces as polynomials.

• STARK Proof Generation

  Compiles traces into Plonky3 AIR (Algebraic Intermediate Representation), and proves the constraints using the Fast Reed-Solomon Interactive Oracle Proof of Proximity (FRI) technique.

• STARK Compression and STARK-to-SNARK Proof Recursion

  To produce a constant-size proof, zkMIPS supports first generating a recursive argument to compress STARK proofs, and then wrapping the compressed proof into a SNARK for efficient on-chain verification.

• Verification

  The SNARK proof can be verified on-chain. The STARK proof can be verified on any verification layer for faster optimistic finalization.

Core Innovations

zkMIPS is the world's first MIPS-based zkVM, achieving the industry-leading performance through the following core innovations:

• zkMIPS Compiler

  Implement the first zero-knowledge compiler for MIPS32r2. Convert standard MIPS binaries into constraint systems with deterministic execution traces using proof-system-friendly compilation and PAIR builder.

• "Area Minimization" Chip Design

  zkMIPS partitions circuit constraints into highly segmented chips, strategically minimizing the total layout area while preserving logical completeness. This fine-grained decomposition enables compact polynomial representations with reduced commitment and evaluation overhead, thereby directly optimizing ZKP proof generation efficiency.

• Multiset Hashing for Memory Consistency Checking

  Replaces MerkleTree hashing with Multiset Hashing for memory consistency checks, significantly reducing witness data and enabling parallel verification.

• KoalaBear Prime Field

  Using KoalaBear Prime \(2^{31} - 2^{24} + 1\) instead of 64-bit Goldilocks Prime, accelerating algebraic operations in proofs.

• Hardware Acceleration

  zkMIPS supports AVX2/512 and GPU acceleration. The GPU prover can achieve 5x faster than CPU prover.

• Integrating Cutting-edge Industry Advancements

  zkMIPS constructs its zero-knowledge proof system by integrating Plonky3's optimized Fast Reed-Solomon IOP (FRI) protocol and adapting SP1's circuit builder, recursion compiler, and precompiles for the MIPS architecture.

Target Use Cases

zkMIPS enables universal verifiable computation via STARK proofs, including:

• Bitcoin L2

  GOAT Network is a Bitcoin L2 built on zkMIPS and BitVM2 to improve the scalability and interoperability of Bitcoin.

• ZK-OP (HybridRollups)

  Combines optimistic rollup’s cost efficiency with validity proof verifiability, allowing users to choose withdrawal modes (fast/high-cost vs. slow/low-cost) while enhancing cross-chain capital efficiency.

• Entangled Rollup

  Entanglement of rollups for trustless cross-chain communication, with universal L2 extension resolving fragmented liquidity via proof-of-burn mechanisms (e.g. cross-chain asset transfers).

• zkML Verification Protects sensitive ML model/data privacy (e.g. healthcare), allowing result verification without exposing raw inputs (e.g. doctors validating diagnoses without patient ECG data).

Installation

zkMIPS is now available for Linux and macOS systems.

Requirements

• Git
• Rust (Nightly)

Option 1: Quick Install

To install the zkMIPS toolchain, use the zkmup installer. Simply open your terminal, run the command below, and follow the on-screen instructions:

curl --proto '=https' --tlsv1.2 -sSf https://raw.githubusercontent.com/zkMIPS/toolchain/refs/heads/main/setup.sh | sh

It will:

• Download the zkmup installer.
• Automatically utilize zkmup to install the latest zkMIPS Rust toolchain which has support for the mipsel-zkm-zkvm-elf compilation target.

List all available toolchain versions:

$ zkmup list-available
20250224 20250108 20241217

Now you can run zkMIPS examples or unit tests.

git clone https://github.com/zkMIPS/zkMIPS
cd zkMIPS && cargo test -r

Troubleshooting

The following error may occur:

cargo build --release
cargo: /lib/x86_64-linux-gnu/libc.so.6: version `GLIBC_2.32' not found (required by cargo)
cargo: /lib/x86_64-linux-gnu/libc.so.6: version `GLIBC_2.33' not found (required by cargo)
cargo: /lib/x86_64-linux-gnu/libc.so.6: version `GLIBC_2.34' not found (required by cargo)

Currently, our prebuilt binaries are built for Ubuntu 22.04 and macOS. Systems running older GLIBC versions may experience compatibility issues and will need to build the toolchain from source.

Option 2: Building from Source

For more details, please refer to document toolchain.

Performance

Metrics

To evaluate a zkVM’s performance, two primary metrics are considered: Efficiency and Cost.

Efficiency

The Efficiency, or cycles per instruction, means how many cycles the zkVM can prove in one second. One cycle is usually mapped to one MIPS instruction in the zkVM.

For each MIPS instruction in a shard, it goes through two main phases: the execution phase and the proving phase (to generate the proof).

In the execution phase, the MIPS VM (Emulator) reads the instruction at the program counter (PC) from the program image and executes it to generate execution traces (events). These traces are converted into a matrix for the proving phase. The number of traces depends on the program's instruction sequence - the shorter the sequence, the more efficient the execution and proving.

In the proving phase, the zkMIPS prover uses a Polynomial Commitment Scheme (PCS) — specifically FRI — to commit the execution traces. The proving complexity is determined by the matrix size of the trace table.

Therefore, the instruction sequence size and prover efficiency directly impact overall proving performance.

Cost

Proving cost is a more comprehensive metric that measures the total expense of proving a specific program. It can be approximated as: Prover Efficiency * Unit, Where Prover Efficiency reflects execution performance, and Unit Price refers to the cost per second of the server running the prover.

For example, ethproofs.org provides a platform for all zkVMs to submit their Ethereum mainnet block proofs, which includes the proof size, proving time and proving cost per Mgas (Efficiency * Unit / GasUsed, where the GasUsed is of unit Mgas).

zkVM benchmarks

To facilitate the fairest possible comparison among different zkVMs, we provide the zkvm-benchmarks suite, enabling anyone to reproduce the performance data.

Performance of zkMIPS

The performance of zkMIPS on an AWS r6a.8xlarge instance, a CPU-based server, is presented below:

Note that all the time is of unit millisecond. Define Rate = 100*(SP1 - zkMIPS)/zkMIPS.

Fibonacci

sha2

sha3

Proving with precompile:

big-memory

sha2-chain

sha3-chain

Proving with precompile:

MIPS VM

zkMIPS is a verifiable computation infrastructure based on the MIPS32, specifically designed to provide zero-knowledge proof generation for programs written in Rust. This enhances project auditing and the efficiency of security verification. Focusing on the extensive design experience of MIPS, zkMIPS adopts the MIPS32r2 instruction set. MIPS VM, one of the core components of zkMIPS, is the execution framework of MIPS32r2 instructions. Below we will briefly introduce the advantages of MIPS32r2 over RV32IM and the execution flow of MIPS VM.

Advantages of MIPS32r2 over RV32IM

1. MIPS32r2 is more consistent and offers more complex opcodes

• The J/JAL instructions support jump ranges of up to 256MiB, offering greater flexibility for large-scale data processing and complex control flow scenarios.
• MIPS32r2 has rich set of bit manipulation instructions and additional conditional move instructions (such as MOVZ and MOVN) that ensure precise data handling.
• MIPS32r2 has integer multiply-add/sub instructions, which can improve arithmetic computation efficiency.
• MIPS32r2 has SEH and SEB sign extension instructions, which make it very convenient to perform sign extension operations on char and short type data.

2. MIPS32r2 has a more established ecosystem

• All instructions in MIPS32r2, as a whole, have been very mature and widely used for more than 20 years. There will be no compatibility issues between ISA modules. And there will be no turmoil caused by manufacturer disputes.
• MIPS has been successfully applied to Optimism's Fraud Proof VM

Execution Flow of MIPS VM

The execution flow of MIPS VM is as follows: 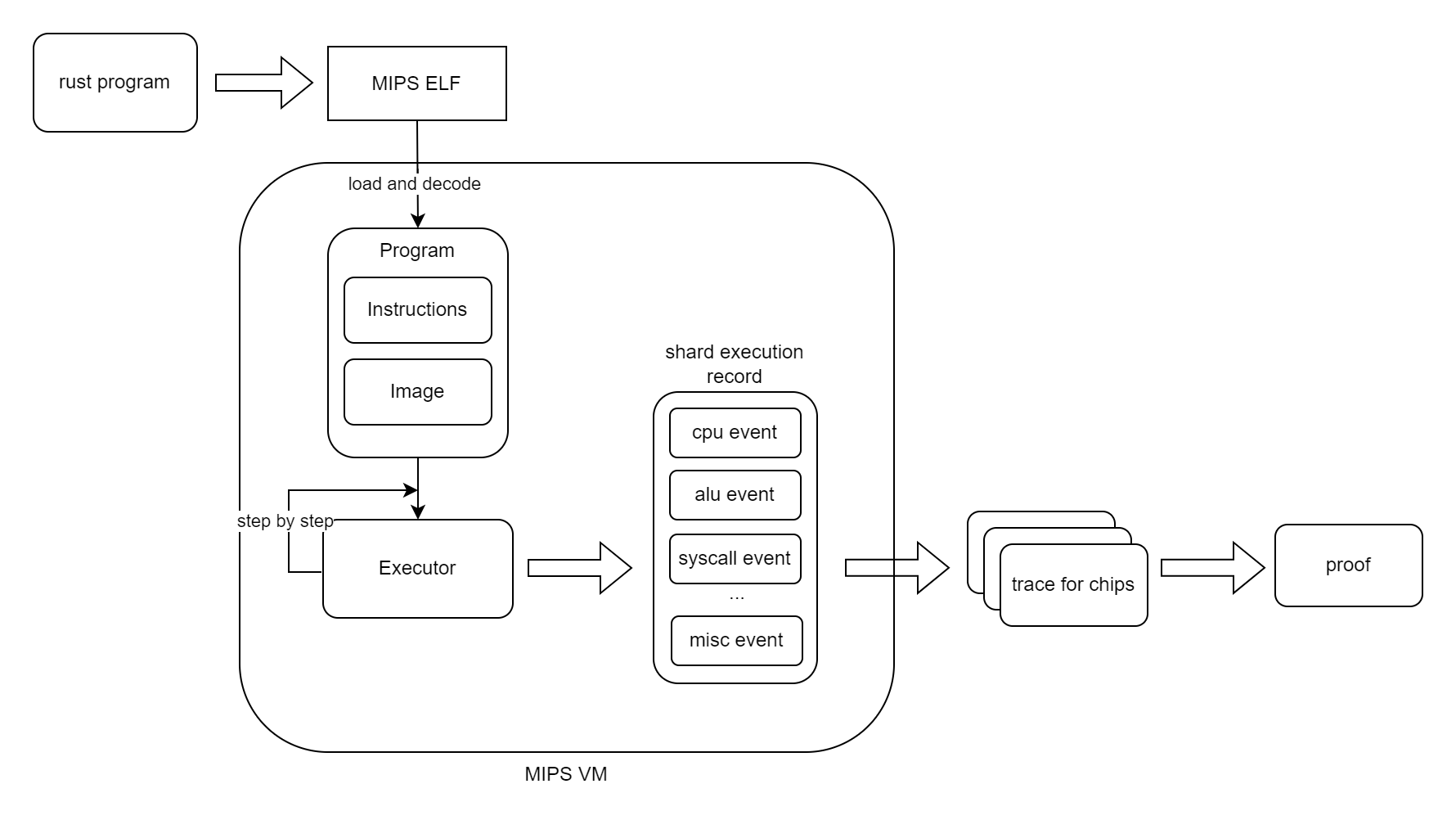Before the execution process of MIPS VM, a Rust program written by the developer is first transformed by a dedicated compiler into the MIPS instruction set, generating a corresponding ELF binary file. This process accurately maps the high-level logic of the program to low-level instructions, laying a solid foundation for subsequent verification.

MIPS VM employs a specially designed executor to simulate the execution of the ELF file:

1. First，the ELF code is loaded into Program, where all data is loaded into the memory image, and all the code is decoded and added into the Instruction List.
2. Then, MIPS VM executes the Instruction and update the ISA states step by step, which is started from the entry point of the ELF and ended with exit condition is triggered. A complete execution record with different type of events is recorded in this process. The whole program will be divided into several shards based on the shape of the execution record.

After the execution process of MIPS VM, the execution record will be used by the prover to generate zero-knowledge proof:

• The events recorded in execution record will be used to generate different traces by different chips.
• This traces serve as the core data for generating the zero-knowledge proof, ensuring that the proof accurately reflects the real execution of the compiled program.

MIPS ISA

The Opcode enum organizes MIPS instructions into several functional categories, each serving a specific role in the instruction set:

#![allow(unused)]
fn main() {
pub enum Opcode {
    // ALU
    ADD = 0,         // ADDSUB
    SUB = 1,         // ADDSUB
    MULT = 2,        // MUL
    MULTU = 3,       // MUL
    MUL = 4,         // MUL
    DIV = 5,         // DIVREM
    DIVU = 6,        // DIVREM
    SLL = 7,         // SLL
    SRL = 8,         // SR
    SRA = 9,         // SR
    ROR = 10,        // SR
    SLT = 11,        // LT
    SLTU = 12,       // LT
    AND = 13,        // BITWISE
    OR = 14,         // BITWISE
    XOR = 15,        // BITWISE
    NOR = 16,        // BITWISE
    CLZ = 17,        // CLO_CLZ
    CLO = 18,        // CLO_CLZ
    // Control Flow
    BEQ = 19,        // BRANCH
    BGEZ = 20,       // BRANCH
    BGTZ = 21,       // BRANCH
    BLEZ = 22,       // BRANCH
    BLTZ = 23,       // BRANCH
    BNE = 24,        // BRANCH
    Jump = 25,       // JUMP
    Jumpi = 26,      // JUMP
    JumpDirect = 27, // JUMP
    // Memory Op
    LB = 28,         // LOAD
    LBU = 29,        // LOAD
    LH = 30,         // LOAD
    LHU = 31,        // LOAD
    LW = 32,         // LOAD
    LWL = 33,        // LOAD
    LWR = 34,        // LOAD
    LL = 35,         // LOAD
    SB = 36,         // STORE
    SH = 37,         // STORE
    SW = 38,         // STORE
    SWL = 39,        // STORE
    SWR = 40,        // STORE
    SC = 41,         // STORE
    // Syscall
    SYSCALL = 42,    // SYSCALL
    // Misc
    MEQ = 43,        // MOVCOND
    MNE = 44,        // MOVCOND
    TEQ = 45,        // MOVCOND
    SEXT = 46,       // SEXT
    WSBH = 47,       // MISC
    EXT = 48,        // EXT
    MADDU = 49,      // MADDSUB
    MSUBU = 50,      // MADDSUB
    INS = 51,        // INS
    UNIMPL = 0xff,
}
}

All MIPS instructions can be divided into the following taxonomies:

ALU Operators
This category includes the fundamental arithmetic logical operations and count operations. It covers addition (ADD) and subtraction (SUB), several multiplication and division variants (MULT, MULTU, MUL, DIV, DIVU), as well as bit shifting and rotation operations (SLL, SRL, SRA, ROR), comparison operations like set less than (SLT, SLTU) a range of bitwise logical operations (AND, OR, XOR, NOR) and count operations like CLZ counts the number of leading zeros, while CLO counts the number of leading ones. These operations are useful in bit-level data analysis.

Memory Operations
This category is dedicated to moving data between memory and registers. It contains a comprehensive set of load instructions—such as LH (load halfword), LWL (load word left), LW (load word), LB (load byte), LBU (load byte unsigned), LHU (load halfword unsigned), LWR (load word right), and LL (load linked)—as well as corresponding store instructions like SB (store byte), SH (store halfword), SWL (store word left), SW (store word), SWR (store word right), and SC (store conditional). These operations ensure that data is correctly and efficiently read from or written to memory.

Branching Instructions
Instructions BEQ (branch if equal), BGEZ (branch if greater than or equal to zero), BGTZ (branch if greater than zero), BLEZ (branch if less than or equal to zero), BLTZ (branch if less than zero), and BNE (branch if not equal) are used to change the flow of execution based on comparisons. These instructions are vital for implementing loops, conditionals, and other control structures.

Jump Instructions
Jump-related instructions, including Jump, Jumpi, and JumpDirect, are responsible for altering the execution flow by redirecting it to different parts of the program. They are used for implementing function calls, loops, and other control structures that require non-sequential execution, ensuring that the program can navigate its code dynamically.

Syscall Instructions
SYSCALL triggers a system call, allowing the program to request services from the zkvm operating system. The service can be a precompiles computation, such as do sha extend operation by SHA_EXTEND precompile. it also can be input/output operation such as SYSHINTREADYSHINTREAD and WRITE.

Misc Instructions
This category includes other instructions. TEQ is typically used to test equality conditions between registers. MADDU/MSUBU is used for multiply accumulation. SEB/SEH is for data sign extended. EXT/INS is for bits extraction and insertion.

Supported instructions

The support instructions are as follows:

Supported syscalls

In essence, the “computation problem” in zkMIPS is the given program, and its “solution” is the execution trace produced when running that program. This trace details every step of the program execution, with each row corresponding to a single step (or a cycle) and each column representing a fixed CPU variable or register state.

Proving a program essentially involves checking that every step in the trace aligns with the corresponding instruction and the expected logic of the MIPS program, convert the traces to polynomials and commit the polynomials by proof system.

Below is the workflow of zkMIPS.

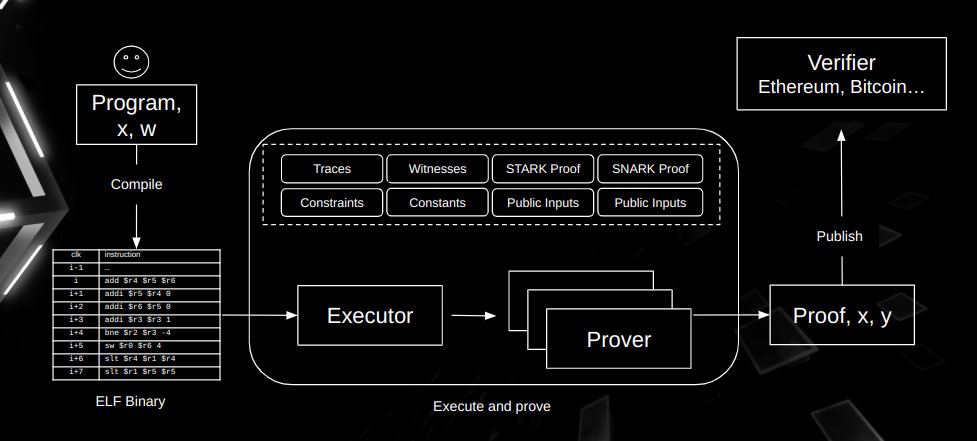
High-Level Workflow of zkMIPS

Referring to the above diagram, zkMIPS follows a structured pipeline composed of the following stages:

1. Guest Program
   A program that written in a high-level language such as Rust or C/C++, creating the application logic that needs to be proved.

2. MIPS Compiler
   The high-level program is compiled into a MIPS ELF binary using a dedicated compiler. This step compiles the program into MIPS32R2 ELF binary.

3. ELF Loader
   The ELF Loader reads and interprets the ELF file and prepares it for execution within the MIPS VM. This includes loading code, initializing memory, and setting up the program’s entry point.

4. MIPS VM
   The MIPS Virtual Machine simulates a MIPS CPU to run the loaded ELF file. It captures every step of execution—including register states, memory accesses, and instruction addresses—and generates the execution trace (i.e., a detailed record of the entire computation).

5. Execution Trace
   This trace is the core data structure used to verify the program. Each row represents a single step of execution, and each column corresponds to a particular CPU register or state variable. By ensuring that every step in the trace matches the intended behavior of the MIPS instructions, zkMIPS can prove the program was executed correctly.

6. Prover
   The Prover takes the execution trace from the MIPS VM and generates a zero-knowledge proof. This proof shows that the program followed the correct sequence of states without revealing any sensitive internal data. In addition, the proof is eventually used by a Verifier Contract or another verification component, often deployed on-chain, to confirm that the MIPS program executed as claimed.

7. Verifier Apart from the native verifier for the generated proof, zkMIPS also offers a solidity verifier for EVM-compatible blockchains.

Prover Internal Proof Generation Steps

Within the Prover, zkMIPS employs multiple stages to efficiently process and prove the execution trace, ultimately producing a format suitable for on-chain verification:

1. Shard
   To prevent memory overflow, a guest program may be split into multiple shards, allowing generation of a proof for each smaller table and then combining the proofs across tables to verify the full program execution.

2. Chip
   Each instruction in a shard generates one or more events (e.g., CPU and ALU events), where each event corresponds to a specific chip (CpuChip, AddSubChip, etc.) - with its own set of constraints.

3. Lookup
   Lookup serves two key purposes:

   • Cross-Chip Communication - The chip needs to send the logic which itself cannot verify to other chips for verification.
   • Consistency of memory access (the data read by the memory is the data written before) - Proving that the read and write data are “permuted”.

   zkMIPS implements these two lookup arguments through LogUp and multiset hashing hashing respectively.

4. Core Proof
   The core proof includes a set of shard proofs.

5. Compressed Proof
   The core proof (a vector of shard proofs) is aggregated into a single compressed proof via the FRI recursive folding algorithm.

6. SNARK Proof
   The compressed proof is further processed using either the Plonk or Groth16 algorithm, resulting in a final Plonk proof or Groth16 proof.

In conclusion, throughout this process, zkMIPS seamlessly transforms a high-level program into MIPS instructions, runs those instructions to produce an execution trace, and then applies STARK, LogUp, PLONK, and Groth16 techniques to generate a succinct zero-knowledge proof. This proof can be verified on-chain to ensure both the correctness and the privacy of the computation.

Program

The setting of zkMIPS is that Prover runs a public program on private inputs and wants to convince Verifier that the program has executed correctly and produces an asserted output, without revealing anything about the computation’s input or intermediate state.

We consider all the inputs as private, the program and output should be public.

The program can be separated into 2 parts from a developer's perspective, the program to be proved and the program to prove. The former program we call it guest, and the latter is host.

Host Program

In a zkMIPS application, the host is the machine that is running the zkVM. The host is an untrusted agent that sets up the zkVM environment and handles inputs/outputs during execution for guest.

Example: Fibonacci

This host program sends the input n = 1000 to the guest program for proving knowledge of the Nth Fibonacci number without revealing the computational path.

use zkm_sdk::{include_elf, utils, ProverClient, ZKMProofWithPublicValues, ZKMStdin};

/// The ELF we want to execute inside the zkVM.
const ELF: &[u8] = include_elf!("fibonacci");

fn main() {
    // Create an input stream and write '1000' to it.
    let n = 1000u32;

    // The input stream that the guest will read from using `zkm_zkvm::io::read`. Note that the
    // types of the elements in the input stream must match the types being read in the program.
    let mut stdin = ZKMStdin::new();
    stdin.write(&n);

    // Create a `ProverClient` method.
    let client = ProverClient::new();

    // Execute the guest using the `ProverClient.execute` method, without generating a proof.
    let (_, report) = client.execute(ELF, stdin.clone()).run().unwrap();
    println!("executed program with {} cycles", report.total_instruction_count());

    // Generate the proof for the given program and input.
    let (pk, vk) = client.setup(ELF);
    let mut proof = client.prove(&pk, stdin).run().unwrap();

    // Read and verify the output.
    //
    // Note that this output is read from values committed to in the program using
    // `zkm_zkvm::io::commit`.
    let n = proof.public_values.read::<u32>();
    let a = proof.public_values.read::<u32>();
    let b = proof.public_values.read::<u32>();

    println!("n: {}", n);
    println!("a: {}", a);
    println!("b: {}", b);

    // Verify proof and public values
    client.verify(&proof, &vk).expect("verification failed");
}

For more details, please refer to document prover.

Guest Program

In zkMIPS, the guest program is the code that will be executed and proven by the zkVM.

Any program written in C, Go, Rust, etc. can be compiled into a MIPS R3000 big-endian ELF executable file using a universal MIPS compiler, that satisfies the required specification.

zkMIPS provides Rust runtime libraries for guest programs to handle input/output operations:

• zkm_zkvm::io::read::<T> (for reading structured data)
• zkm_zkvm::io::commit::<T> (for committing structured data)

Note that type T must implement both serde::Serialize and serde::Deserialize. For direct byte-level operations, use the following methods to bypass serialization and reduce cycle counts:

• zkm_zkvm::io::read_vec (raw byte reading)
• zkm_zkvm::io::commit_slice (raw byte writing)

Guest Program Example

zkMIPS supports multiple programming languages. Below are examples of guest programs written in Rust and C/C++.

Rust Example: Fibonacci

//! A simple program that takes a number `n` as input, and writes the `n-1`th and `n`th Fibonacci
//! number as output.

// These two lines are necessary for the program to properly compile.
//
// Under the hood, we wrap your main function with some extra code so that it behaves properly
// inside the zkVM.
#![no_std]
#![no_main]
zkm_zkvm::entrypoint!(main);

pub fn main() {
    // Read an input to the program.
    //
    // Behind the scenes, this compiles down to a system call which handles reading inputs
    // from the prover.
    let n = zkm_zkvm::io::read::<u32>();

    // Write n to public input
    zkm_zkvm::io::commit(&n);

    // Compute the n'th fibonacci number, using normal Rust code.
    let mut a = 0;
    let mut b = 1;
    for _ in 0..n {
        let mut c = a + b;
        c %= 7919; // Modulus to prevent overflow.
        a = b;
        b = c;
    }

    // Write the output of the program.
    //
    // Behind the scenes, this also compiles down to a system call which handles writing
    // outputs to the prover.
    zkm_zkvm::io::commit(&a);
    zkm_zkvm::io::commit(&b);
}

C/C++ Example: Fibonacci_C

For non-Rust languages, you can compile them to static libraries and link them in Rust by FFI. For example:

extern "C" {
    unsigned int add(unsigned int a, unsigned int b) {
        return a + b;
    }
}

unsigned int modulus(unsigned int a, unsigned int b) {
    return a % b;
}

//! A simple program that takes a number `n` as input, and writes the `n-1`th and `n`th fibonacci
//! number as an output.

// These two lines are necessary for the program to properly compile.
//
// Under the hood, we wrap your main function with some extra code so that it behaves properly
// inside the zkVM.
#![no_std]
#![no_main]
zkm_zkvm::entrypoint!(main);

// Use add function from Libexample.a
extern "C" {
    fn add(a: u32, b: u32) -> u32;
    fn modulus(a: u32, b: u32) -> u32;
}

pub fn main() {
    // Read an input to the program.
    //
    // Behind the scenes, this compiles down to a system call which handles reading inputs
    // from the prover.
    let n = zkm_zkvm::io::read::<u32>();

    // Write n to public input
    zkm_zkvm::io::commit(&n);

    // Compute the n'th fibonacci number, using normal Rust code.
    let mut a = 0;
    let mut b = 1;
    unsafe {
        for _ in 0..n {
            let mut c = add(a, b);
            c = modulus(c, 7919); // Modulus to prevent overflow.
            a = b;
            b = c;
        }
    }

    // Write the output of the program.
    //
    // Behind the scenes, this also compiles down to a system call which handles writing
    // outputs to the prover.
    zkm_zkvm::io::commit(&a);
    zkm_zkvm::io::commit(&b);
}

Compiling Guest Program

Now you need compile your guest program to an ELF file that can be executed in the zkVM.

To enable automatic building of your guest crate when compiling/running the host crate, create a build.rs file in your host/ directory (adjacent to the host crate's Cargo.toml) that utilizes the zkm-build crate.

.
├── guest
└── host
    ├── build.rs # Add this file
    ├── Cargo.toml
    └── src

build.rs:

fn main() {
    zkm_build::build_program("../guest");
}

And add zkm-build as a build dependency in host/Cargo.toml:

[build-dependencies]
zkm-build = "1.0.0"

Advanced Build Options

The build process using zkm-build can be configured by passing a BuildArgs struct to the build_program_with_args() function.

For example, you can use the default BuildArgs to batch compile guest programs in a specified directory.

use std::io::{Error, Result};
use std::io::path::PathBuf;

use zkm_build::{build_program_with_args, BuildArgs};

fn main() -> Result<()> {
    let tests_path = [env!("CARGO_MANIFEST_DIR"), "guests"]
        .iter()
        .collect::<PathBuf>()
        .canonicalize()?;

    build_program_with_args(
        tests_path
            .to_str()
            .ok_or_else(|| Error::other(format!("expected {guests_path:?} to be valid UTF-8")))?,
            BuildArgs::default(),
    );

    Ok(())
}

Prover

The zkm_sdk crate provides all the necessary tools for proof generation. Key features include the ProverClient, enabling you to:

• Initialize proving/verifying keys via setup().
• Execute your program via execute().
• Generate proofs with prove().
• Verify proofs through verify().

When generating Groth16 or PLONK proofs, the ProverClient automatically downloads the pre-generated proving key (pk) from a trusted setup by calling try_install_circuit_artifacts().

Example: Fibonacci

The following code is an example of using zkm_sdk in host.

use zkm_sdk::{include_elf, utils, ProverClient, ZKMProofWithPublicValues, ZKMStdin};

/// The ELF we want to execute inside the zkVM.
const ELF: &[u8] = include_elf!("fibonacci");

fn main() {
    // Create an input stream and write '1000' to it.
    let n = 1000u32;

    // The input stream that the guest will read from using `zkm_zkvm::io::read`. Note that the
    // types of the elements in the input stream must match the types being read in the program.
    let mut stdin = ZKMStdin::new();
    stdin.write(&n);

    // Create a `ProverClient` method.
    let client = ProverClient::new();

    // Execute the guest using the `ProverClient.execute` method, without generating a proof.
    let (_, report) = client.execute(ELF, stdin.clone()).run().unwrap();
    println!("executed program with {} cycles", report.total_instruction_count());

    // Generate the proof for the given program and input.
    let (pk, vk) = client.setup(ELF);
    let mut proof = client.prove(&pk, stdin).run().unwrap();

    // Read and verify the output.
    //
    // Note that this output is read from values committed to in the program using
    // `zkm_zkvm::io::commit`.
    let n = proof.public_values.read::<u32>();
    let a = proof.public_values.read::<u32>();
    let b = proof.public_values.read::<u32>();

    println!("n: {}", n);
    println!("a: {}", a);
    println!("b: {}", b);

    // Verify proof and public values
    client.verify(&proof, &vk).expect("verification failed");
}

Proof Types

zkMIPS provides customizable proof generation options:

#![allow(unused)]
fn main() {
/// A proof generated with zkMIPS of a particular proof mode.
#[derive(Debug, Clone, Serialize, Deserialize, EnumDiscriminants, EnumTryAs)]
#[strum_discriminants(derive(Default, Hash, PartialOrd, Ord))]
#[strum_discriminants(name(ZKMProofKind))]
pub enum ZKMProof {
    /// A proof generated by the core proof mode.
    ///
    /// The proof size scales linearly with the number of cycles.
    #[strum_discriminants(default)]
    Core(Vec<ShardProof<CoreSC>>),
    /// A proof generated by the compress proof mode.
    ///
    /// The proof size is constant, regardless of the number of cycles.
    Compressed(Box<ZKMReduceProof<InnerSC>>),
    /// A proof generated by the Plonk proof mode.
    Plonk(PlonkBn254Proof),
    /// A proof generated by the Groth16 proof mode.
    Groth16(Groth16Bn254Proof),
}
}

Core Proof (Default)

The default prover mode generates a sequence of STARK proofs whose cumulative proof size scales linearly with the execution trace length.

#![allow(unused)]
fn main() {
let client = ProverClient::new();
client.prove(&pk, stdin).run().unwrap();
}

Compressed Proof

The compressed proving mode generates constant-sized STARK proofs, but not suitable for on-chain verification.

#![allow(unused)]
fn main() {
let client = ProverClient::new();
client.prove(&pk, stdin).compressed().run().unwrap();
}

Groth16 Proof (Recommended)

The Groth16 proving mode ​generates succinct SNARK proofs with a compact size of approximately 260 bytes, ​and features on-chain verification.

#![allow(unused)]
fn main() {
let client = ProverClient::new();
client.prove(&pk, stdin).groth16().run().unwrap();
}

PLONK Proof

The PLONK proving mode generates succinct SNARK proofs with a compact size of approximately 868 bytes, while maintaining on-chain verifiability. In contrast to Groth16, PLONK removes the dependency on trusted setup ceremonies.

#![allow(unused)]
fn main() {
let client = ProverClient::new();
client.prove(&pk, stdin).plonk().run().unwrap();
}

Hardware Acceleration

zkMIPS provides hardware acceleration support for AVX256/AVX512 on x86 CPUs due to support in Plonky3.

You can check your CPU's AVX compatibility by running:

grep avx /proc/cpuinfo

Check if you can see avx2 or avx512 in the results.

To activate AVX256 optimization, add these flags to your RUSTFLAGS environment variable:

RUSTFLAGS="-C target-cpu=native" cargo run --release

To activate AVX512 optimization, add these flags to your RUSTFLAGS environment variable:

RUSTFLAGS="-C target-cpu=native -C target-feature=+avx512f" cargo run --release

Network Prover

We support the use of a network prover via the ZKM proof network, accessible through our RESTful API. By default, it uses the Groth16 proving mode. >The proving process consists of several stages: queuing, splitting, proving, aggregating and finalizing. Each stage involves a varying duration.

Requirements

• CA certificate: ca.pem, ca.key.
• Register your address to gain access.
• Use zkm_sdk from our project template:

zkm-sdk = { git = "https://github.com/zkMIPS/zkm-project-template", branch = "main", features = ["snark"] }

Environment Variable Setup

Before running your application, make sure to export the required environment variable to enable the network prover. Here's an example:

export ZKM_PROVER=${ZKM_PROVER-"network"}
export RUST_LOG=${RUST_LOG-info}
export SEG_SIZE=${SEG_SIZE-65536}
export OUTPUT_DIR=${BASEDIR}/output
export EXECUTE_ONLY=false

##network proving
export CA_CERT_PATH=${BASEDIR}/tool/ca.pem
export CERT_PATH=${BASEDIR}/tool/cert.pem
export KEY_PATH=${BASEDIR}/tool/key.pem
##The private key corresponding to the public key when registering in the https://www.zkm.io/apply
export PROOF_NETWORK_PRVKEY=
export ENDPOINT=https://152.32.186.45:20002    ##the test entry of zkm proof network
export DOMAIN_NAME=stage

Example

The following is an example of using the network prover on the host:

const ELF: &[u8] = include_bytes!(env!("ZKM_ELF_bitvm2-covenant"));
#[tokio::main]
async fn main() -> anyhow::Result<()> {
    env_logger::try_init().unwrap_or_default();

    //  Directory for output files
    let output_dir = env::var("OUTPUT_DIR").unwrap_or(String::from("./output"));
    let seg_size = env::var("SEG_SIZE").unwrap_or("262144".to_string());
    let seg_size = seg_size.parse::<_>().unwrap_or(262144);
    let execute_only = env::var("EXECUTE_ONLY").unwrap_or("false".to_string());
    let execute_only = execute_only.parse::<bool>().unwrap_or(false);

    // Network endpoint, should be: https://152.32.186.45:20002
    let endpoint = env::var("ENDPOINT").map_or(None, |endpoint| Some(endpoint.to_string()));
    let ca_cert_path = env::var("CA_CERT_PATH").map_or(None, |path| Some(path.to_string()));
    let cert_path = env::var("CERT_PATH").map_or(None, |x| Some(x.to_string()));
    // The private key path of the certificate
    let key_path = env::var("KEY_PATH").map_or(None, |x| Some(x.to_string()));
    let domain_name = Some(env::var("DOMAIN_NAME").unwrap_or("stage".to_string()));
    // The private key of the proof network, which is used to sign the proof.
    let proof_network_privkey =
        env::var("PROOF_NETWORK_PRVKEY").map_or(None, |x| Some(x.to_string()));

    // Create configuration for the prover client
    let prover_cfg = ClientCfg {
        zkm_prover_type: "network".to_string(),
        endpoint,
        ca_cert_path,
        cert_path,
        key_path,
        domain_name,
        proof_network_privkey,
    };
    let prover_client = ProverClient::new(&prover_cfg).await;

    let mut prover_input = ProverInput {
        elf: Vec::from(ELF),
        seg_size,
        execute_only,
        ..Default::default()
    };
    // If the guest program doesn't have inputs, it doesn't need the setting.
    set_guest_input(&mut prover_input);
    
    // Proving
    let proving_result = prover_client.prover.prove(&prover_input, None).await;
    
    // Write the proof to the output directory
    match proving_result {
        Ok(Some(prover_result)) => {
            if !execute_only {
                if prover_result.proof_with_public_inputs.is_empty() {
                    log::info!(
                        "Fail: snark_proof_with_public_inputs.len() is : {}.Please try setting SEG_SIZE={}",
                        prover_result.proof_with_public_inputs.len(), seg_size/2
                    );
                }
                let output_path = Path::new(&output_dir);
                let proof_result_path =
                    output_path.join("snark_proof_with_public_inputs.json");
                let mut f = file::new(&proof_result_path.to_string_lossy());
                match f.write(prover_result.proof_with_public_inputs.as_slice()) {
                    Ok(bytes_written) => {
                        log::info!("Proof: successfully written {} bytes.", bytes_written);
                    }
                    Err(e) => {
                        log::info!("Proof: failed to write to file: {}", e);
                    }
                }
                log::info!("Generating proof successfully.");
            } else {
                log::info!("Generating proof successfully .The proof is not saved.");
            }
        }
        Ok(None) => {
            log::info!("Failed to generate proof.The result is None.");
        }
        Err(e) => {
            log::info!("Failed to generate proof. error: {}", e);
        }
    }
    Ok(())
}

fn set_guest_input(prover_input: &mut ProverInput) {
    // Combine all the inputs into a two-dimensional array
    let mut private_input: Vec<Vec<u8>> = vec![];

    let goat_withdraw_txid: Vec<u8> =
        hex::decode(std::env::var("GOAT_WITHDRAW_TXID").unwrap_or("32bc8a6c5b3649f92812c461083bab5e8f3fe4516d792bb9a67054ba040b7988".to_string())).unwrap();
    write_to_guest_private_input(&mut private_input, &goat_withdraw_txid);
    
    // Encode private input into a one-dimensional array and pass it to the proof network.
    let mut pri_buf = Vec::new();
    bincode::serialize_into(&mut pri_buf, &private_input).expect("private_input serialization failed");
    prover_input.private_inputstream = pri_buf;
}

[!NOTE] The proof network uses stdin.write_vec() to write private input data to the guest program. If your guest program uses zkm_zkvm::io::read(); to read this input, you must serialize it before pushing to the private input:

#![allow(unused)]
fn main() {
fn write_to_guest_private_input(private_input: &mut Vec<Vec<u8>>, data: &[u8]) {
    let mut tmp = Vec::new();
    bincode::serialize_into(&mut tmp, data).expect("serialization failed");
    private_input.push(tmp);
}
}

Proof Composition

What is a receipt?

A receipt gives the results of your program along with proof that they were produced honestly.

What is Proof Composition

You can verify other receipts in the guest use zkm_zkvm::lib::verify::verify_zkm_proof()

Example: Aggregation

Host

//! A simple example showing how to aggregate proofs of multiple programs with ZKM.

use zkm_sdk::{
    include_elf, HashableKey, ProverClient, ZKMProof, ZKMProofWithPublicValues, ZKMStdin,
    ZKMVerifyingKey,
};

/// A program that aggregates the proofs of the simple program.
const AGGREGATION_ELF: &[u8] = include_elf!("aggregation");

/// A program that just runs a simple computation.
const FIBONACCI_ELF: &[u8] = include_elf!("fibonacci");

/// An input to the aggregation program.
///
/// Consists of a proof and a verification key.
struct AggregationInput {
    pub proof: ZKMProofWithPublicValues,
    pub vk: ZKMVerifyingKey,
}

fn main() {
    // Setup the logger.
    zkm_sdk::utils::setup_logger();

    // Initialize the proving client.
    let client = ProverClient::new();

    // Setup the proving and verifying keys.
    let (aggregation_pk, _) = client.setup(AGGREGATION_ELF);
    let (fibonacci_pk, fibonacci_vk) = client.setup(FIBONACCI_ELF);

    // Generate the fibonacci proofs.
    let proof_1 = tracing::info_span!("generate fibonacci proof n=10").in_scope(|| {
        let mut stdin = ZKMStdin::new();
        stdin.write(&10);
        client.prove(&fibonacci_pk, stdin).compressed().run().expect("proving failed")
    });
    let proof_2 = tracing::info_span!("generate fibonacci proof n=20").in_scope(|| {
        let mut stdin = ZKMStdin::new();
        stdin.write(&20);
        client.prove(&fibonacci_pk, stdin).compressed().run().expect("proving failed")
    });
    let proof_3 = tracing::info_span!("generate fibonacci proof n=30").in_scope(|| {
        let mut stdin = ZKMStdin::new();
        stdin.write(&30);
        client.prove(&fibonacci_pk, stdin).compressed().run().expect("proving failed")
    });

    // Setup the inputs to the aggregation program.
    let input_1 = AggregationInput { proof: proof_1, vk: fibonacci_vk.clone() };
    let input_2 = AggregationInput { proof: proof_2, vk: fibonacci_vk.clone() };
    let input_3 = AggregationInput { proof: proof_3, vk: fibonacci_vk.clone() };
    let inputs = vec![input_1, input_2, input_3];

    // Aggregate the proofs.
    tracing::info_span!("aggregate the proofs").in_scope(|| {
        let mut stdin = ZKMStdin::new();

        // Write the verification keys.
        let vkeys = inputs.iter().map(|input| input.vk.hash_u32()).collect::<Vec<_>>();
        stdin.write::<Vec<[u32; 8]>>(&vkeys);

        // Write the public values.
        let public_values =
            inputs.iter().map(|input| input.proof.public_values.to_vec()).collect::<Vec<_>>();
        stdin.write::<Vec<Vec<u8>>>(&public_values);

        // Write the proofs.
        //
        // Note: this data will not actually be read by the aggregation program, instead it will be
        // witnessed by the prover during the recursive aggregation process inside zkMIPS itself.
        for input in inputs {
            let ZKMProof::Compressed(proof) = input.proof.proof else { panic!() };
            stdin.write_proof(*proof, input.vk.vk);
        }

        // Generate the plonk bn254 proof.
        client.prove(&aggregation_pk, stdin).plonk().run().expect("proving failed");
    });
}

Guest

//! A simple program that aggregates the proofs of multiple programs proven with the zkVM.

#![no_main]
zkm_zkvm::entrypoint!(main);

use sha2::{Digest, Sha256};

pub fn main() {
    // Read the verification keys.
    let vkeys = zkm_zkvm::io::read::<Vec<[u32; 8]>>();

    // Read the public values.
    let public_values = zkm_zkvm::io::read::<Vec<Vec<u8>>>();

    // Verify the proofs.
    assert_eq!(vkeys.len(), public_values.len());
    for i in 0..vkeys.len() {
        let vkey = &vkeys[i];
        let public_values = &public_values[i];
        let public_values_digest = Sha256::digest(public_values);
        zkm_zkvm::lib::verify::verify_zkm_proof(vkey, &public_values_digest.into());
    }

    // TODO: Do something interesting with the proofs here.
    //
    // For example, commit to the verified proofs in a merkle tree. For now, we'll just commit to
    // all the (vkey, input) pairs.
    let commitment = commit_proof_pairs(&vkeys, &public_values);
    zkm_zkvm::io::commit_slice(&commitment);
}

pub fn words_to_bytes_le(words: &[u32; 8]) -> [u8; 32] {
    let mut bytes = [0u8; 32];
    for i in 0..8 {
        let word_bytes = words[i].to_le_bytes();
        bytes[i * 4..(i + 1) * 4].copy_from_slice(&word_bytes);
    }
    bytes
}

/// Encode a list of vkeys and committed values into a single byte array. In the future this could
/// be a merkle tree or some other commitment scheme.
///
/// ( vkeys.len() || vkeys || committed_values[0].len as u32 || committed_values[0] || ... )
pub fn commit_proof_pairs(vkeys: &[[u32; 8]], committed_values: &[Vec<u8>]) -> Vec<u8> {
    assert_eq!(vkeys.len(), committed_values.len());
    let mut res = Vec::with_capacity(
        4 + vkeys.len() * 32
            + committed_values.len() * 4
            + committed_values.iter().map(|vals| vals.len()).sum::<usize>(),
    );

    // Note we use big endian because abi.encodePacked in solidity does also
    res.extend_from_slice(&(vkeys.len() as u32).to_be_bytes());
    for vkey in vkeys.iter() {
        res.extend_from_slice(&words_to_bytes_le(vkey));
    }
    for vals in committed_values.iter() {
        res.extend_from_slice(&(vals.len() as u32).to_be_bytes());
        res.extend_from_slice(vals);
    }

    res
}

Precompiles

Precompiles are built into the zkMIPS to optimize the performance of zero-knowledge proofs (ZKPs) and related cryptographic operations. The goal is to enable more efficient handling of complex cryptographic tasks that would otherwise be computationally expensive if implemented in smart contracts.

Within the zkVM, precompiles are made available as system calls executed through the syscall MIPS instruction. Each precompile is identified by a distinct system call number and provides a specific computational interface.

Specification

For advanced users, it's possible to directly interact with the precompiles through external system calls.

Here is a list of all available system calls & precompiles.

#![allow(unused)]
fn main() {
//! Syscalls for the zkMIPS zkVM.
//!
//! Documentation for these syscalls can be found in the zkVM entrypoint
//! `zkm_zkvm::syscalls` module.

pub mod bls12381;
pub mod bn254;
pub mod ed25519;
pub mod hasher;
pub mod io;
pub mod keccak;
pub mod secp256k1;
pub mod secp256r1;
pub mod unconstrained;
pub mod utils;
#[cfg(feature = "verify")]
pub mod verify;
extern "C" {
    /// Halts the program with the given exit code.
    pub fn syscall_halt(exit_code: u8) -> !;

    /// Writes the bytes in the given buffer to the given file descriptor.
    pub fn syscall_write(fd: u32, write_buf: *const u8, nbytes: usize);

    /// Reads the bytes from the given file descriptor into the given buffer.
    pub fn syscall_read(fd: u32, read_buf: *mut u8, nbytes: usize);

    /// Executes the SHA-256 extend operation on the given word array.
    pub fn syscall_sha256_extend(w: *mut [u32; 64]);

    /// Executes the SHA-256 compress operation on the given word array and a given state.
    pub fn syscall_sha256_compress(w: *mut [u32; 64], state: *mut [u32; 8]);

    /// Executes an Ed25519 curve addition on the given points.
    pub fn syscall_ed_add(p: *mut [u32; 16], q: *const [u32; 16]);

    /// Executes an Ed25519 curve decompression on the given point.
    pub fn syscall_ed_decompress(point: &mut [u8; 64]);

    /// Executes an Sepc256k1 curve addition on the given points.
    pub fn syscall_secp256k1_add(p: *mut [u32; 16], q: *const [u32; 16]);

    /// Executes an Secp256k1 curve doubling on the given point.
    pub fn syscall_secp256k1_double(p: *mut [u32; 16]);

    /// Executes an Secp256k1 curve decompression on the given point.
    pub fn syscall_secp256k1_decompress(point: &mut [u8; 64], is_odd: bool);

    /// Executes an Secp256r1 curve addition on the given points.
    pub fn syscall_secp256r1_add(p: *mut [u32; 16], q: *const [u32; 16]);

    /// Executes an Secp256r1 curve doubling on the given point.
    pub fn syscall_secp256r1_double(p: *mut [u32; 16]);

    /// Executes an Secp256r1 curve decompression on the given point.
    pub fn syscall_secp256r1_decompress(point: &mut [u8; 64], is_odd: bool);

    /// Executes a Bn254 curve addition on the given points.
    pub fn syscall_bn254_add(p: *mut [u32; 16], q: *const [u32; 16]);

    /// Executes a Bn254 curve doubling on the given point.
    pub fn syscall_bn254_double(p: *mut [u32; 16]);

    /// Executes a BLS12-381 curve addition on the given points.
    pub fn syscall_bls12381_add(p: *mut [u32; 24], q: *const [u32; 24]);

    /// Executes a BLS12-381 curve doubling on the given point.
    pub fn syscall_bls12381_double(p: *mut [u32; 24]);

    /// Executes the Keccak Sponge
    pub fn syscall_keccak_sponge(input: *const u32, result: *mut [u32; 17]);

    /// Executes an uint256 multiplication on the given inputs.
    pub fn syscall_uint256_mulmod(x: *mut [u32; 8], y: *const [u32; 8]);

    /// Executes a 256-bit by 2048-bit multiplication on the given inputs.
    pub fn syscall_u256x2048_mul(
        x: *const [u32; 8],
        y: *const [u32; 64],
        lo: *mut [u32; 64],
        hi: *mut [u32; 8],
    );
    /// Enters unconstrained mode.
    pub fn syscall_enter_unconstrained() -> bool;

    /// Exits unconstrained mode.
    pub fn syscall_exit_unconstrained();

    /// Defers the verification of a valid zkMIPS zkVM proof.
    pub fn syscall_verify_zkm_proof(vk_digest: &[u32; 8], pv_digest: &[u8; 32]);

    /// Returns the length of the next element in the hint stream.
    pub fn syscall_hint_len() -> usize;

    /// Reads the next element in the hint stream into the given buffer.
    pub fn syscall_hint_read(ptr: *mut u8, len: usize);

    /// Allocates a buffer aligned to the given alignment.
    pub fn sys_alloc_aligned(bytes: usize, align: usize) -> *mut u8;

    /// Decompresses a BLS12-381 point.
    pub fn syscall_bls12381_decompress(point: &mut [u8; 96], is_odd: bool);

    /// Computes a big integer operation with a modulus.
    pub fn sys_bigint(
        result: *mut [u32; 8],
        op: u32,
        x: *const [u32; 8],
        y: *const [u32; 8],
        modulus: *const [u32; 8],
    );

    /// Executes a BLS12-381 field addition on the given inputs.
    pub fn syscall_bls12381_fp_addmod(p: *mut u32, q: *const u32);

    /// Executes a BLS12-381 field subtraction on the given inputs.
    pub fn syscall_bls12381_fp_submod(p: *mut u32, q: *const u32);

    /// Executes a BLS12-381 field multiplication on the given inputs.
    pub fn syscall_bls12381_fp_mulmod(p: *mut u32, q: *const u32);

    /// Executes a BLS12-381 Fp2 addition on the given inputs.
    pub fn syscall_bls12381_fp2_addmod(p: *mut u32, q: *const u32);

    /// Executes a BLS12-381 Fp2 subtraction on the given inputs.
    pub fn syscall_bls12381_fp2_submod(p: *mut u32, q: *const u32);

    /// Executes a BLS12-381 Fp2 multiplication on the given inputs.
    pub fn syscall_bls12381_fp2_mulmod(p: *mut u32, q: *const u32);

    /// Executes a BN254 field addition on the given inputs.
    pub fn syscall_bn254_fp_addmod(p: *mut u32, q: *const u32);

    /// Executes a BN254 field subtraction on the given inputs.
    pub fn syscall_bn254_fp_submod(p: *mut u32, q: *const u32);

    /// Executes a BN254 field multiplication on the given inputs.
    pub fn syscall_bn254_fp_mulmod(p: *mut u32, q: *const u32);

    /// Executes a BN254 Fp2 addition on the given inputs.
    pub fn syscall_bn254_fp2_addmod(p: *mut u32, q: *const u32);

    /// Executes a BN254 Fp2 subtraction on the given inputs.
    pub fn syscall_bn254_fp2_submod(p: *mut u32, q: *const u32);

    /// Executes a BN254 Fp2 multiplication on the given inputs.
    pub fn syscall_bn254_fp2_mulmod(p: *mut u32, q: *const u32);

}
}

Guest Example: syscall_sha256_extend

In the guest program, you can call the precompile syscall_sha256_extend() in the following way:

#![allow(unused)]
fn main() {
zkm_zkvm::syscalls::syscall_sha256_extend
}

The complete code is as follows:

#![no_std]
#![no_main]
zkm_zkvm::entrypoint!(main);

use zkm_zkvm::syscalls::syscall_sha256_extend;

pub fn main() {
    let mut w = [1u32; 64];
    syscall_sha256_extend(&mut w);
    syscall_sha256_extend(&mut w);
    syscall_sha256_extend(&mut w);
    println!("{:?}", w);
}

Patched Crates

Patching a crate refers to replacing the implementation of a specific interface within the crate with a corresponding zkVM precompile, which can achieve significant performance improvements.

Supported Crates

Using Patched Crates

There are two approaches to using patched crates:

Option 1: Directly add the patched crates as dependencies in the guest program's Cargo.toml. For example:

[dependencies]
sha2 = { git = "https://github.com/zkMIPS-patches/RustCrypto-hashes.git", package = "sha2", branch = "patch-sha2-0.10.8" }

Option 2: Add the appropriate patch entries to your guest's Cargo.toml. For example:

[dependencies]
sha2 = "0.10.8"

[patch.crates-io]
sha2 = { git = "https://github.com/zkMIPS-patches/RustCrypto-hashes.git", package = "sha2", branch = "patch-sha2-0.10.8" }

When patching a crate from a GitHub repository rather than crates.io, you need to explicitly declare the source repository in the patch section. For example:

[dependencies]
ed25519-dalek = { git = "https://github.com/dalek-cryptography/curve25519-dalek" }

[patch."https://github.com/dalek-cryptography/curve25519-dalek"]
ed25519-dalek = { git = "https://github.com/zkMIPS-patches/curve25519-dalek", branch = "patch-4.1.3" }

How to Patch a Crate

First, implement the target precompile in zkVM (e.g., syscall_keccak_sponge) with full circuit logic. Given the implementation complexity, we recommend submitting an issue for requested precompiles.

Then replace the target crate's existing implementation with the zkVM precompile (e.g., syscall_keccak_sponge). For example, we have reimplemented keccak256 by syscall_keccak_sponge, and use this implementation to replace keccak256 in the revm crate.

#![allow(unused)]
fn main() {
use zkm_zkvm::lib::keccak256::keccak256 as keccak256_zkvm;

// Define the keccak256 function
#[inline]
pub fn keccak256<T: AsRef<[u8]>>(bytes: T) -> B256 {
    cfg_if::cfg_if! {
        if #[cfg(target_os = "zkvm")] {
            let output = keccak256_zkvm(bytes.as_ref());
            B256::from(output)
        } else {
            keccak256_alloy(bytes)
        }
    }
}
}

Finally, we can use the new keccak256 in the revme guest lib, which the revme guest depends on.

Design

As ​MIPS instruction set based zkVM, zkMIPS is designed to generate efficient zero-knowledge proofs for complex computations (e.g., smart contract execution). Its architecture integrates a ​modular state machine, ​custom chip design, and a ​hybrid proof system (STARK + SNARK).

• Modular State Machine

  The state machine serves as the central control unit, simulating MIPS instruction execution through ​multi-chip collaboration to ensure all state transitions are verifiable in zero-knowledge. Key submodules include the Program Chip, CPU Chip, Memory Chips, ALU Chips, Global Chip and Bytes Chip. Together they enforce equivalence between MIPS program execution and zkMIPS VM constraints.

• Custom Chip Design

  zkMIPS translates MIPS execution traces into a polynomial constraint system. To efficiently encode MIPS instructions:

  • Dedicated constraint circuits are implemented for each MIPS opcode to accelerate proof generation.
  • Precompiled chips handle ​common yet computationally intensive cryptographic operations (e.g., hashing, field arithmetic) for optimal performance.

• Hybrid Proof System

  zkMIPS employs a three-stage proof workflow to balance modularity and efficiency:

  • Sharded STARK Proofs:

    MIPS instructions are partitioned into fixed-length shards, each verified via fast STARK proofs.

  • Recursive Aggregation:

    Shard proofs are compressed using a recursive STARK composition scheme.

  • SNARK Finalization:

    The aggregated proof is wrapped into a Groth16-compatible SNARK for efficient on-chain verification.

  • Proof Composition

    Proof composition enables developers to implement recursive proof verification, allowing cryptographic proofs to be nested within zkVM programs.

State Machine

The zkMIPS state machine is a ​MIPS-compatible, register-based virtual machine designed for zero-knowledge verification of general-purpose computations. It operates as a modular system of interconnected chips/tables (terms used interchangeably), each specializing in distinct computational tasks.

Core Components:

• Program Chip

  Manages program counter (PC) and instruction stream decoding while enforcing strict PC progression aligned with MIPS pipeline stages. The program table is preprocessed and constrains the program counter, instructions and selectors for the program. The CPU chip looks up its instructions in the Program chip.

• ​CPU Chip

  The CPU chip serves as the central processing unit for MIPS instruction execution. Each clock cycle corresponds to a table row, indexed via the pc column from the Program chip. We constrain the transition of the pc, clk and operands in this table according to the cycle’s instruction. Each MIPS instruction has three operands: a, b, and c, and the CPU table has a separate column for the value of each of these three operands. The CPU table has no constraints for the proper execution of the instruction, nor does the table itself check that operand values originate from (or write to) correct memory addresses. zkMIPS relies on cross-table lookups to verify these constraints.

• ALU Chips

  The ALU chips manage common field operations and bitwise operations. These chips are responsible for verifying correctness of arithmetic and bitwise operations and throug corss-table lookups from the main CPU chip to make sure executing the correct instructions.

• Flow-Control Chips

  Flow control mechanisms are ​fundamental components in modern computer programs, ​enhancing program functionality and execution flexibility by providing structured control mechanisms. In the zkMIPS, ​dedicated modules — ​the Branch chip and Jump chip — ​are implemented to handle branch instructions and jump instructions ​respectively within the MIPS Instruction Set Architecture (ISA).

• ​Memory Chips

  Memory chips are responsible for the values in the a, b, and c operand columns in CPU chip come from (or write to) the right memory addresses specified in the instruction. zkMIPS use multiset hashing based offline memory consistency checking in the main operation of its memory argument with several memory tables.

• Global Chip

  Global chip in zkMIPS is responsible for processing and verifying global lookup events (such as memory accesses, system calls), ensuring compliance with predefined rules and generating cryptographic proof data.

• Custom Chips

  Several Custom chips are used to accelecate proving time in zkMIPS's proof system: Poseidon2 hash, STARK compression and STARK-to-SNARK adapter.

• Precompiled Chips:

  Precompiled chips are custom-designed chips for accelerating non-MIPS cryptographic operations in zkMIPS. They are recommended for handling common yet computationally intensive cryptographic tasks, such as SHA-256/Keccak hashing, elliptic curve operations (e.g., BN254, Secp256k1), and pairing-based cryptography.

Each chip consists of an AIR (Algebraic Intermediate Representation) to enforce functional correctness and received/sent signal vectors to connect with other chips. This modular design enables collaborative verification of MIPS instruction execution with full computational completeness, cryptographic security, and ​optimized proving performance featuring parallelizable constraint generation and sublinear verification complexity.

CPU

The CPU chip handles the core logic for processing MIPS instructions. Each program cycle corresponds to a table row accessed via the pc column in the preprocessed Program table. Constraints on pc transitions, clock cycles, and operand handling are enforced through column-based verification.

The CPU architecture employs a structured column-based design to manage instruction execution, branching/jump logic, memory operations, and system calls. Key components are organized into specialized modules (represented as specific columns in the CPU table) with clearly defined constraints and interactions. The CPU table uses selector columns to distinguish instruction types and perform corresponding constraint validation.

Column Classification

The CPU columns in zkMIPS encapsulate the core execution context of MIPS instructions within the zkVM. Key components include:

• ​Shard Management​​: Tracks execution shards for cross-shard operations like syscalls and memory access.
• Clock System​​: Tracks the global clock cycles.
• ​Program Counter​​: Sequential validation via pc, next_pc, and next_next_pc for instruction flow correctness.
• Instruction Decoding​​: Stores opcode, operands, and immediate flags.
• ​Memory Access​​: Validates read/write operations through memory corresponding columns.
• ​Control Flags​​: Identifies instruction types and operand constraints.
• ​Operand Validation​​: Enforces register/immediate selection and zero-register checks.

​Constraint Categories​​

zkMIPS's CPU constraints ensure instruction integrity across four key dimensions:

• Flow Constraints​​

  • Program counter continuity: Ensures sequential instruction flow continuity via program counter validation.
  • Clock synchronization: Synchronizes timing mechanisms for system operations.

• ​​Operand Constraints​​

  Validates operand sources (register/immediate distinction) and enforces zero-value rules under specific conditions.

• ​Memory Consisetency Constraints​​

  Address validity: Verify memory address validity. Value consistency: Verify memory consistency checking.

• ​Execution Context Constraints​​

  Instruction exclusivity: Maintains instruction type exclusivity. Real-row validation: Enforces operational validity flags for non-padded execution.

These constraints are implemented through AIR polynomial identities, cross-table lookup arguments, boolean assertions, and multi-set hashing ensuring verifiable MIPS execution within zkMIPS's zkVM framework.

Memory

The Memory chip family manages memory operations in the MIPS execution environment through specialized column-based constraints. It covers five core subsystems: MemoryGlobal, MemoryLocal, MemoryProgram, MemoryAccess, and MemoryInstructions. Together, they enforce the correct execution of MIPS memory operations.

MemoryGlobal

Handles cross-shard memory management, initialization/finalization of global memory blocks, enforcement of address continuity, and verification of zero-register protection

Major Columns:

• ​Address Tracking: Monitors shard ID and 32-bit memory addresses, while enforcing sequential order.
• ​Value Validation: Stores 4-byte memory values with byte-level decomposition.
• ​Control Flags: Identify valid operations and mark terminal addresses in access sequences.
• ​Zero-Register Protection: Flags operations targeting protected memory regions.

Key Constraints:

• Addresses must follow strict ascending order verified via 32-bit comparator checks.
• Memory at address 0 remains immutable after initialization.
• Cross-shard finalization requires consistency with Global chip.

MemoryLocal

Maintains single-shard memory operations, tracking read/write events within a shard and preserving initial and final value consistency between consecutive shards.

Major Columns:

• ​Shard Identification: Tracks initial/final shard IDs for multi-shard transitions.
• ​Temporal Metadata: Records start/end clock cycles of memory operations.
• ​Value States: Preserves original and modified values for atomicity checks.
• ​Time Difference Limbs: Splits clock differentials for range verification.

Key Constraints:

• Final values must correspond to explicit write operations.
• Overlapping accesses require a minimum 1-clock gap between operations.
• Decomposed bytes must recompose to valid 32-bit words.

MemoryProgram

Responsible for locking executable code into immutable memory regions during proof generation, preventing runtime modification.

Major Columns:

• ​Address-Value Binding: Maps fixed addresses to preloaded executable code.
• Lock Flags: Enforces write protection for program memory regions.
• Multiplicity Checks: Ensures single initialization of static memory.

Key Constraints:

• Preloaded addresses cannot be modified during runtime.
• Each code shard address must be initialized exactly once.
• Access attempts to locked regions trigger validation failures.

MemoryAccess

Ensures global state synchronization, maintaining memory coherence across shards via multiset hashing.

Major Columns:

• ​Previous State Tracking: Stores prior shard ID and timestamp for dependency checks.
• Time Difference Analysis: Splits timestamp gaps into 16-bit and 8-bit components.
• Shard Transition Flags: Differentiate intra-shard vs. cross-shard operations.

Key Constraints:

• Cross-shard operations must reference valid prior states.
• Timestamp differences must be constrained within 24-bit range (16+8 bit decomposition).
• Intra-shard operations require sequential clock progression.

MemoryInstructions

Validates MIPS load/store operations, verifying semantics of memory-related instructions (e.g., LW, SW, LB) and alignment rules.

Major Columns:

• ​Instruction Type Flags: Identifies various memory operations (LW/SB/SC/etc.).
• ​Address Alignment: Tracks least-significant address bits for format checks.
• ​Sign Conversion: Manages sign-extension logic for narrow-width loads.
• ​Atomic Operation Bindings: Establishes linkage between load-linked (LL) to store-conditional (SC) events.

Key Constraints:

• Word operations (LW/SW) require 4-byte alignment (enforced by verifying last 2 address bits = 0).
• Signed loads (LB/LH) perform extension using most significant bit/byte.
• SC operations succeed only if memory remains unchanged since the corresponding LL.
• Address ranges are validated through bitwise decomposition checks.

ALU

The Arithmetic Logic Unit (ALU) chips comprise ​​specialized verification circuits​​ designed to enforce computational correctness for all arithmetic and bitwise operations. These circuits implement ​​cross-table lookup protocols​​ with the main CPU table, ensuring instruction-execution integrity throughout the processor pipeline.

Modular Design

The ALU employs a ​​hierarchical verification architecture​​ organized by MIPS instruction class:

• ​AddSub Chip​​ - Validates addition/subtraction instructions (ADD, ADDI, SUB, SUBU).
• ​Bitwise Chip​​ - Verifies logical operations (AND, ANDI, OR, XOR, NOR).
• ​​CloClz Chip​​ - Processes count-leading-ones/zeros operations (CLO/CLZ).
• ​​DivRem Chip​​ - Implements division/remainder operations (DIV/REM).
• ​​Lt Chip​​ - Enforces signed/unsigned comparisons (SLT, SLTI, SLTU).
• ​​Mul Chip​​ - Handles multiplication operations (MUL, MULT, MULTU).
• ​​ShiftLeft Chip​​ - Executes logical left shifts (SLL, SLLI).
• ​​ShiftRight Chip​​ - Manages logical/arithmetic right shifts (SRL, SRA). ​

Each chip employs domain-specific verification to ensure accurate execution of programmed instructions and LogUp-based proper alignment with CPU table constraints, thereby guaranteeing consistency between computational results and predefined operational logic.

In Section arithmetization, we analyze the AddSub Chip to demonstrate its ​​column architecture​​ and ​​constraint system implementation​​, providing concrete insights into ALU verification mechanisms.

Flow Control

zkMIPS enforces MIPS32r2 control flow verification via dedicated Branch and Jump chips, ensuring precise execution of program control instructions.

Branch Chip

MIPS branch instructions execute conditional jumps through register comparisons (BEQ/BNE for equality, BGTZ/BLEZ etc. for sign checks). They calculate targets using 16-bit offsets shifted left twice (enabling ±128KB jumps) and feature a mandatory branch delay slot that always executes the next instruction—simplifying pipelining by allowing compiler-controlled optimizations.

Structure Description

Branch chip uses columns to record the following information.

• ​Control Flow Management​​

  • Tracks current and future program counter states across sequential and branching execution paths (pc, next_pc,target_pc,next_next_pc).
  • Implements 32-bit address validation through dedicated range-checking components(next_pc_range_checker, target_pc_range_checker, next_next_pc_range_checker).

• ​Operand Handling System​​

  • Stores three register/immediate values following MIPS three-operand convention (op_a_value, op_b_value, op_c_value).
  • Contains special flag detection for zero-register operand scenarios (op_a_0).

• ​​Instruction Semantics Encoding​​

  Embeds five mutually exclusive flags corresponding to MIPS branch opcodes (is_beq, is_bltz, is_blez, is_bgtz, is_bgez).

• ​Execution State Tracking​​

  Maintains dual execution path indicators for taken/not-taken branch conditions(is_branching, not_branching).

• ​Comparison Logic Core​​

  Evaluates signed integer relationships between primary operands, generating equality, greater-than, and less-than condition flags (a_eq_b, a_gt_b, a_lt_b).

Major Constraints

We use the following key constraints to validate the branch chip:

• Program Counter Validation

  • Range check for all PC values (pc, next_pc, target_pc, next_next_pc, etc.).
  • Branching case: next_pc must equal target_pc.
  • Non-branching case: next_next_pc must equal next_pc + 4.
  • is_branching and not_branching are mutually exclusive and exhaustive for real instructions.

• Instruction Validity

  • Exactly one branch instruction flag must be active per row (1 = is_beq + ... + is_bgtz).
  • Instruction flags are strictly boolean values (0/1).
  • Opcode validity is enforced through linear combination verification.

• Branch Condition Logic is_branching and not_branching consistent whti condition flags.

Jump Chip

MIPS jump instructions force unconditional PC changes via absolute or register-based targets. They calculate 256MB-range addresses by combining PC's upper bits with 26-bit immediates or use full 32-bit register values. All jumps enforce a ​mandatory delay slot executing the next instruction—enabling compiler-driven pipeline optimizations without speculative execution.

Structure Description

Jump chip uses columns to record the following information:

• ​Control Flow Management​​

  • Tracks current program counter and jump targets (pc, next_pc, target_pc).
  • Implements 32-bit address validation via dedicated range checkers (next_pc_range_checker, target_pc_range_checker, op_a_range_checker).

• ​​Operand System​​

  • Stores three operands for jump address calculation (op_a_value, op_b_value, op_c_value).
  • Contains zero-register flag detection for first operand register (op_a_0).

• ​​Instruction Semantics​​

  Embeds three mutually exclusive jump-type flags (is_jump, is_jumpi, is_jumpdirect).

Major Constraints

We use the fllowing key constraints to validate the jump chip:

• Instruction Validity

  • Exactly one jump instruction flag must be active per row:

    #![allow(unused)]
    fn main() {
    1 = is_jump + is_jumpi + is_jumpdirect
    }

  • Instruction flags are strictly boolean (0/1).

  • Opcode validity enforced through linear combination verification:

    #![allow(unused)]
    fn main() {
    opcode = is_jump*JUMP + is_jumpi*JUMPI + is_jumpdirect*JUMPDIRECT
    }

• Return Address Handling

  • For non-X0 register targets (op_a_0 = 0):

    #![allow(unused)]
    fn main() {
    op_a_value = next_pc + 4
    }

  • When jumping to X0 (op_a_0 = 1), return address validation is skipped.

• Range Checking

  All critical values (op_a_value, next_pc, target_pc) are range-checked, ensuring values are valid 32-bit words.

• PC Transition Logic

  • Target_pc calculation via ALU operation:

    #![allow(unused)]
    fn main() {
    send_alu(
      Opcode::ADD,
      target_pc = next_pc + op_b_value, 
      is_jumpdirect
    )
    }

  • Direct jumps (is_jumpdirect) use immediate operand addition.

Other Components

Except for CPU chip, Memory chips, and ALU chips, we also have Program chip, Bytes chip, customized Poseidon2 chip, STARK Compression chip, STARK-to-SNARK chip, and Precompiled chips.

In addition to the CPU, Memory, and ALU chips, zkMIPS incorporates several specialized components:

• ​Program Chip - Manages instruction preprocessing
• Global Chip - Processes global cross-table lookups
• Bytes Chip - Handles byte operations and u16 range check
• Poseidon2 Hash Chip - Cryptographic primitive implementation
• ​STARK Compression/SNARK-to-SNARK Adapter - Proof system optimization
• ​Precompiled Chips - Accelerated cryptographic operations

Program Chip

Program chip establishes program execution constraints through preprocessed instruction verification. The CPU chip performs lookups against this verified instruction set.

Global Chip

Global chip in zkMIPS is responsible for processing and verifying global lookup events (such as memory accesses, system calls), ensuring compliance with predefined rules and generating zero-knowledge data commitments.

Bytes Chip

The Bytes chip is a preprocessed table that performs 8/16-bit unsigned integer range checks and byte logic/arithmetic operations.

Poseidon2 Hash Chip

Poseidon2 enhances the original Poseidon sponge function architecture with dual operational modes: maintaining sponge construction for general hashing while incorporating domain-specific compression mechanisms. Core optimizations include:

• Matrix-based linear layer substitutions replacing partial rounds.
• Configurable function width/rate parameters.

zkMIPS's implementation integrates specialized permutation logic with KoalaBear field arithmetic optimizations, critical for proof compression layers and STARK-to-SNARK proof system interoperability.

​STARK Compression/SNARK-to-SNARK Adapter

Three proofs are used in zkMIPS

• Shard Proofs: Used to verify correct execution of patched MIPS instructions (i.e., shard).
• STARK Compressed Proof: Compress shard proofs into one STARK proof.
• STARK-to-SNARK Adapter: Transform final STARK proof into Groth16-compatible SNARK proof.

After emulating MIPS instructions into STARK circuits, where each circuit processes fixed-length instruction shards, and after deriving the corresponding shard STARK proofs, these proofs are first compressed into a single STARK proof. This consolidated proof is then transformed into a SNARK proof. The chips responsible for STARK compression and the STARK-to-SNARK adapter are custom-designed specifically for proof verification over the KoalaBear field.

Precompiled Chips

Another category of chips extensively utilized in zkMIPS is Precompiled chips. These chips are specifically designed to handle widely used but computationally intensive cryptographic operations, such as hash functions and signature schemes.

Unlike the approach of emulating MIPS instructions, zkMIPS delegates these computations to dedicated precompiled tables. The CPU table then performs lookups to retrieve the appropriate values from these tables (precompiled operations are activated via syscalls). Precompiles have the capability to directly read from and write to memory through the memory argument. They are typically provided with a clock (clk) value and pointers to memory addresses, which specify the locations for reading or writing data during the operation. For a comprehensive list of precompiled tables, refer to this section.

Arithmetization

Algebraic Intermediate Representation (AIR) serves as the arithmetization foundation in the zkMIPS system, bridging computation and succinct cryptographic proofs. AIR provides a structured method to represent computations through polynomial constraints over execution traces.

Key Concepts of AIR

• Execution Trace

  A tabular structure where each row represents system's state at a computation step, with columns corresponding to registers/variables.

• Transition Constraints

  Algebraic relationships enforced between consecutive rows, expressed as low-degree polynomials (e.g., \(P(state_i, state_{i+1}) = 0\)).

• Boundary Constraints

  Ensure valid initial/final states (e.g., \(state_0 = initial\_value\)).

These constraints utilize low-degree polynomials for efficient proof generation/verification. zkMIPS mandates degree-3 polynomial constraints within its AIR framework, establishing a formally verifiable equilibrium between proof generation efficiency and trace column representation compactness. See AIR paper for rigorous technical details.

AIR Implementation in zkMIPS Chips

Having introduced various chip/table structures in zkMIPS, we note that building a chip involves:

• Matrix Population - Filling values into a matrix structure.
• Constraint Construction - Establishing relationships between values, particularly across consecutive rows.

This process aligns with AIR's core functionality by:

• Treating column values as polynomial evaluations.
• Encoding value constraints as polynomial relationships.

AddSub Chip Example

Supported MIPS Instructions

Column Structure

#![allow(unused)]
fn main() {
pub struct AddSubCols<T> {
    // Program flow
    pub pc: T,          
    pub next_pc: T,    
    
    // Core operation
    pub add_operation: AddOperation<T>,  // Shared adder for both ops (a = b + c)
    
    // Input operands (context-sensitive):
    // - ADD: operand_1 = b, operand_2 = c 
    // - SUB: operand_1 = a, operand_2 = c
    pub operand_1: Word<T>,  
    pub operand_2: Word<T>,
    
    // Validation flags
    pub op_a_not_0: T,  // Non-zero guard for first operand
    pub is_add: T,      // ADD opcode flag
    pub is_sub: T,      // SUB opcode flag
}

pub struct AddOperation<T> {
    pub value: Word<T>,
    pub carry: [T; 3],
}
// 32-bit word structure
pub struct Word<T>(pub [T; WORD_SIZE]); // WORD_SIZE = 4
}

The AddSub Chip implementation utilizes 20 columns：

• operand_1.[0-3], operand_2.[0-3]: 4-byte operands (8 columns),
• add_operation.value.[0-3]: 4-byte results (4 columns),
• add_operation.carry.[0-2]: Carry flags (3 columns),
• pc, next_pc, op_a_not_0, is_add, is_sub: Control signals (5 columns).

Computational Validity Constraints

The corresponding constraints support (we use op_1, op_2, add_op for short of operand_1, operand_2 and add_operation respectively):

• Zero Constraints

  Enforces add/sub validity for each byte, e.g., for addition \(op\_1.0 + op\_2.0 - add\_op.value.0 = 0 \) or \(op\_1.0 + op\_2.0 - add\_op.value.0 = 256 \).

• bool constraints

  carry values are bool, e.g., \( add\_op.carry.0 \in \{0,1\} \).

• range check 8-bits values for op_1.i, op_2.i, add_op.value.i. e.g., \(op\_1.0 \in \{0,1,2,\cdots,255\}\).

Matrix Polulation

Sample register state evolution:

Instructions 1, 2, 3, 4, and 6 are integrated with the AddSub Chip. The trace matrix (illustrated below, with the final row highlighting polynomial constraints) delineates their computational pathways.

AIR Transformation Example

Each column is represented as a polynomial defined over a ​​2-adic subgroup​​ within the ​​KoalaBear prime field​​. To demonstrate AIR expression, we analyze the ​​first-byte computation​​ in the addition operation:

\[P_{add}(x) := (j(x) + n(x) - c(x))(j(x) + n(x) - c(x)-256) = 0.\]

And for sub operation, \[P_{sub}(x) := (j(x) + n(x) - c(x))(j(x) + n(x) - c(x)-256) = 0.\]

Using operation selectors \(s(x), t(x)\), the derived polynomila constraint is \[ s(x)\cdot P_{add}(x) + t(x) \cdot P_{sub}(x) = 0.\]

Where:

• s(x): Add operation selector,
• t(x): Sub operation selector,
• j(x): First byte of op_1,
• n(x): First byte of op_2,
• c(x): First byte of result value add_op.value.

Preprocessed AIR

For invariant components (e.g., Program/Bytes chips), zkMIPS precomputes commitments to invariant data columns and predefines fixed AIR constraints among them during setup to establish the Preprocessed AIR framework. By removing redundant recomputation of preprocessed AIR constraints in proofs, PAIR reduces ZKP proving time.

Conclusion

The AIR framework transforms trace constraints into polynomial identities, where increased rows only expand the evaluation domain rather than polynomial complexity. zkMIPS also enhances efficiency through:

• Lookup Tables for range checks.
• Multiset Hashing for memory consistency.
• FRI for polynomial interactive oracle proofs (IOP).

These components constitute the foundational architecture of zkMIPS and will be elaborated in subsequent sections.

Lookup Arguments

Lookup arguments allow generating cryptographic proofs showing that elements from a witness vector belong to a predefined table (public or private). Given:

• Table \(T = \{t_i\}\), where \(i=0,…,N−1 \) (public/private)
• Lookups \(F = \{f_j\}\), where \(j=0,…,M−1 \) (private witness)

The protocol proves \(F \subseteq T \), ensuring all witness values adhere to permissible table entries.

Since its inception, lookup protocols have evolved through continuous optimizations. zkMIPS implements the ​LogUp protocol to enable efficient proof generation.

LogUp

LogUp employs logarithmic derivatives for linear-complexity verification. For a randomly chosen challenge \(\alpha\), the relation \(F \subseteq T\) holds with high probability when: \[ \sum_{i=0}^{M-1} \frac{1}{f_i - \alpha} = \sum_{i=0}^{N-1} \frac{m_i}{t_i - \alpha} \] , where \(m_i\) denotes the multiplicity of \(t_i\) in \(F\). See full protocol details.

LogUp Implementation in zkMIPS

Cross-chip verification in zkMIPS utilizes LogUp for consistency checks, as shown in the dependency diagram:

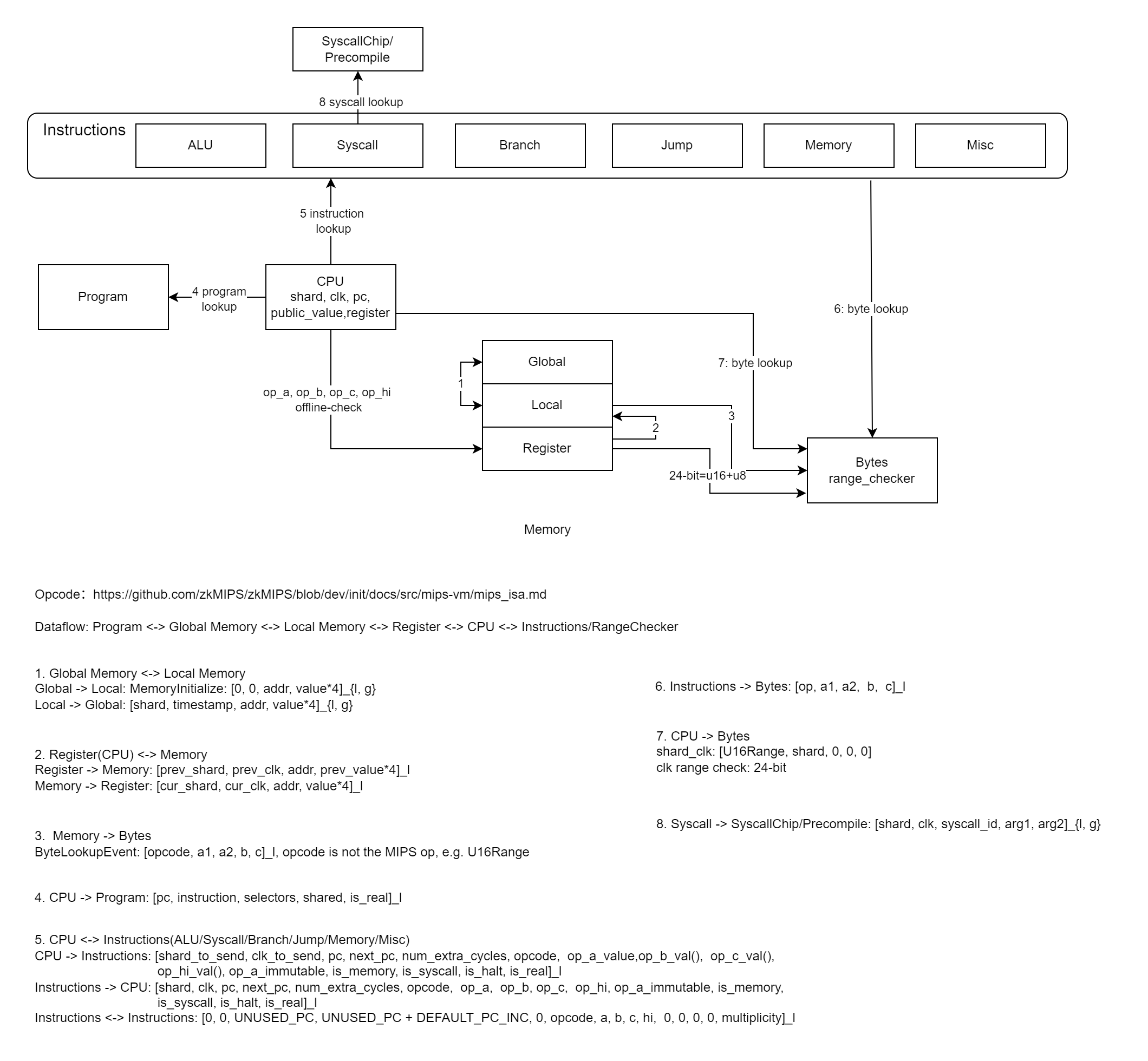
Key Lookup Relationships:

* In the latest implementation, zkMIPS employs multiset-hashing to ensure memory consistency checking, enhancing proof efficiency and modularity.

Range Check Implementation Example

8-bit Range Check Design

In zkMIPS's architecture, 32-bit values undergo byte-wise decomposition into four 8-bit components, with each byte occupying a dedicated memory column. This structural approach enables native support for 8-bit range constraints (0 ≤ value < 255) during critical operations including arithmetic logic unit (ALU) computations and memory address verification.

• Starting Lookup Table (T)

For lookups \(\{f_0, f_1, \dots, f_{M-1}\}\) (all elements in [0, 255]), we:

1. Choose random \(\alpha\);
2. Construct two verification tables.

• Lookups (F)

  f	\(d = 1/(f-\alpha)\)	sum
  \(f_0\)	\(d_0=1/(f_0-\alpha)\)	\(d_0\)
  \(f_1\)	\(d_1=1/(f_1-\alpha)\)	\(d_0 + d_1\)
  \(f_2\)	\(d_2=1/(f_2-\alpha)\)	\(d_0+d_1+d_2\)
  ...	...	...
  \(f_{M-1}\)	\(d_m=1/(f_{M-1}-\alpha)\)	\(\sum_{i=0}^{M-1}d_i\)

• Updated Lookup Table

  t	m	\(d = m/(f+\alpha)\)	sum
  0	\(m_0\)	\(d_0 = m_0/\alpha \)	\(d_0\)
  1	\(m_1\)	\(d_1 = m_1/(1-\alpha)\)	\(d_0 + d_1\)
  2	\(m_2\)	\(d_2 = m_2/(2-\alpha)\)	\(d_0+d_1+d_2\)
  ...	...	...	..
  255	\(m_{255}\)	\(d_{255} = m_{255}/(255-\alpha)\)	\(\sum_{i=0}^{255}d_i\)

,where \(m_i\) denotes the occurrence count of \(i\) in lookups.

LogUp ensures that if the final cumulative sums in both tables match (which is exactly \[ \sum_{i=0}^{M-1} \frac{1}{f_i - \alpha} = \sum_{i=0}^{N-1} \frac{m_i}{t_i - \alpha} \] ), then with high probability every \(f_i\) originates from table \(T\) (i.e., falls within 0-255 range).

Memory Consistency Checking

Offline memory checking is a method that enables a prover to demonstrate to a verifier that a read/write memory was used correctly. In such a memory system, a value \(v\) can be written to an addresses \(a\) and subsequently retrieved. This technique allows the verifier to efficiently confirm that the prover adhered to the memory's rules (i.e., that the value returned by any read operation is indeed the most recent value that was written to that memory address).

This is in contrast to "online memory checking" techniques like Merkle hashing which ​immediately verify that a memory read was done correctly by insisting that each read includes an authentication path. Merkle hashing is ​computationally expensive on a per-read basis for ZK provers, and offline memory checking suffices for zkVM design.

zkMIPS replaces ZKM’s online memory checking with multiset-hashing-based offline memory checking for improved efficiency. zkMIPS's verifies the consistency of read/write operations by constructing a ​read set \(RS\) and a ​write set \(WS\) and proving their equivalence. This mechanism leverages ​multiset hashing on an elliptic curve over KoalaBear Prime's 7th extension field to ensure memory integrity efficiently. Below is a detailed breakdown of its key components.

Construction of Read Set and Write Set

Definition: The read set \(RS\) and write set \(WS\) are sets of tuples \(a, v, c\), where:

• \(a\): Memory address
• \(v\): Value stored at address \(a\)
• \(c\): Operation counter

Three-Stage Construction

Initialization:

• \(RS = WS = \emptyset\);
• All memory cells \(a_i\) are initialized with some value \(v_i\) at op count \(c=0\). Add the initial tuples to the write set \(WS = WS \bigcup \{(a_i, v_i, 0)\}\) for all \(i\).

Read and write operations:

• ​Read Operation, for reading a value from address \(a\):
  • Find the last tuple \((a, v, c)\) added to write set \(WS\) with the address \(a\).
  • \(RS = RS \bigcup \{(a, v, c)\}\) and \(WS = WS \bigcup \{(a, v, c_{now})\}\), with \(c_{now}\) the current op count.
• ​Write Operation, for writing a value \(v'\) to address \(a\):
  • Find the last tuple \((a, v, c)\) added to write set \(WR\) with the address \(a\).
  • \(RS = RS \bigcup \{(a, v, c)\}\) and \(WS = WS \bigcup \{(a, v', c_{now})\}\).

Post-processing：

• For all memory cells \(a_i\), add the last tuple \((a_i, v_i, c_i)\) in write set \(WS\) to \(RS\): \(RS = RS \bigcup \{(a_i, v_i, c_i)\}\).

Core Observation

The prover adheres to the memory rules ​if the following conditions hold:

1. The read and write sets are correctly initialized;
2. For each address \(a_i\), the instruction count added to \(WS\) strictly increases over time;
3. ​For read operations: Tuples added to \(RS\) and \(WS\) must have the same value.
4. ​For write operations: The operation counter of the tuple in \(RS\) must be less than that in \(WS\).
5. After post-processing, \(RS = WS\).

Brief Proof: Consider the first erroneous read memory operation. Assume that a read operation was expected to return the tuple \((a,v,c)\), but it actually returned an incorrect tuple \((a, v' \neq v, c')\) and added it to read set \(RS\). Note that all tuples in \(WS\) are distinct. After adding \((a,v',c_{now})\) to \(WS\), the tuples \((a,v,c)\) and \((a,v',c_{now})\) are not in the read set \(RS\). According to restriction 3, after each read-write operation, there are always at least two tuples in \(WS\) that are not in \(RS\), making it impossible to adjust to \(RS = WS\) through post-processing.

Multiset Hashing

Multiset hashing maps a (multi-)set to a short string, making it computationally infeasible to find two distinct sets with the same hash. The hash is computed incrementally, with ​order-independence as a key property.

Implementation on Elliptic Curve

Consider the group \(G\) as the set of points \((x,y)\) on the elliptic curve \(y^2 = x^3 +Ax+B\) (including the point at infinity). We can implement a hash-to-group approach. To hash a set element into a point on the elliptic curve, we first map the set element to the \(x\)-coordinate of the point. Since this may not be a valid \(x\)-coordinate on the elliptic curve, we add an 8-bit tweak \(t\). Additionally, we constrain the sign of the \(y\)-coordinate to prevent flipping, either by ensuring \(y\) is a quadratic residue or by adding range checks.

In zkMIPS, the following parameters are used.

• KoalaBear Prime field: \(\mathbb{F}_P\), with \(P = 2^{31} - 2^{24} +1\).
• Septic extension field: Defined under irreducible polynomial \( u^7 + 2u -8\).
• Elliptic curve: Defined with \(A = 3*u , B= -3\) (provides ≥102-bit security).
• Hash algorithm: Poseidon2 is used as the hash algorithm.

STARK Protocol

Polynomial Constraint System Architecture

Following arithmetization, the computation is represented through a structured polynomial system.

Core Components

• ​Execution Trace Polynomials

  Encode state transitions across computation steps as: \[ T_i(x) = \sum_{k=0}^{N-1} t_{i,k} \cdot L_k(x),\] where \(L_k(x)\) are Lagrange basis polynomials over domain H. ​

• Constraint Polynomials Encode verification conditions as algebraic relations: \[C_j(x) = R_j(T_1(x),T_2(x), \cdots, T_m(x), T_1(g \cdot x), T_2(g \cdot x), \cdots, T_m(g \cdot x)) = 0,\] for all \(x \in H\), where \(g\) is the generator of H.

Constraint Aggregation

For proof efficiency, we combine constraints using: \[C_{comb}(x) = \sum_j \alpha_j C_j(x),\] where \( \alpha_j\) are derived through the Fiat-Shamir transformation.

Mixed Matrix Commitment Scheme (MMCS)

Polynomial Commitments in STARK

STARK uses Merkle trees for polynomial commitments:

• Setup: No trusted setup is needed, but a hash function for Merkle tree construction must be predefined. We use Poseidon2 as the predefined hash function.

• Commit: Evaluate polynomials at all roots of unity in its domain, construct a Merkle tree with these values as leaves, and publish the root as the commitment.

• Open: The verifier selects a random challenge point, and the prover provides the value and Merkle path for verification.

Batch Commitment Protocol

The "Mixed Matrix Commitment Scheme" (MMCS) is a generalization of a vector commitment scheme used in zkMIPS. It supports:

• Committing to matrices.
• Opening rows.
• Batch operations - committing to multiple matrices simultaneously, even when they differ in dimensions.

When opening a particular row index:

• For matrices with maximum height: use the full row index.
• For smaller matrices: truncate least-significant bits of the index.

These semantics are particularly useful in the FRI protocol.

Low-Degree Extension (LDE)

Suppose the trace polynomials are initially of length \(N\). For security, we evaluate them on a larger domain (e.g., \(2^k \cdot N\)), called the LDE domain.

Using Lagrange interpolation:

• Compute polynomial coefficients.
• Extend evaluations to the larger domain,

zkMIPS implements this via Radix2DitParallel - a parallel FFT algorithm that divides butterfly network layers into two halves.

Low-Degree Enforcement

Quotient Polynomial Construction

To prove \(C_{comb}(x)\) vanishes over subset \(H\), construct quotient polynomial \(Q(x)\): \[Q(x) = \frac{C_{comb}(x)} {Z_{H}(x)} = \frac{\sum_j \alpha_j C_j(x)}{\prod_{h \in H}(x-h)}.\]

The existence of such a low-degree \(Q(x)\) proves \(C_{comb}(x)\) vanishes over \(H\).

FRI Protocol

The Fast Reed-Solomon Interactive Oracle Proof (FRI) protocol proves the low-degree of \(P(x)\). zkMIPS optimizes FRI by leveraging:

• Algebraic structure of quartic extension \(\mathbb{F}_{p^4}\).
• KoalaBear prime field \(p = 2^{31} - 2^{24} + 1\).
• Efficient Poseidon2 hash computation.

Three-Phase FRI Procedure

• Commitment Phase:

  • The prover splits \(P(x)\) into two lower-degree polynomials \(P_0(x)\), \(P_1(x)\), such that: \(P(x) = P_0(x^2) + x \cdot P_1(x^2)\).

  • The verifier sends a random challenge \(\alpha \in \mathbb{F}_{p^4}\)

  • The prover computes a new polynomial: \(P'(x) = P_0(x) + \alpha \cdot P_1(x)\), and sends the commitment of the polynomials to the verifier.

• ​Recursive Reduction:

  • Repeat splitting process for \(P'(x)\).
  • Halve degree each iteration until constant term or degree ≤ d.

• ​Verification Phase:

  • Verifier checks consistency between committed values at random point \(z\) in initial subgroup.

Verifing

Verification contents

Through merkle opening technique, verifier checks the following relation at a randomly chosen point at the LDE domain:

• Confirm correct folding via Merkle proofs.

• Ensure the final polynomial is a constant (or has degree no more than d).

• Proper computation of

  • Constraint polynomials \(C_j(x)\).
  • Combined constraint \(c_{comb}(x)\).

Grinding Factor & Repeating Factor

Given the probabilistic nature of STARK verification, the protocol prevents brute-force attacks by requiring either:

• A Proof of Work (PoW) accompanying each proof, or
• multiple verification rounds.

This approach significantly increases the computational cost of malicious attempts. In zkMIPS, we employ multiple verification rounds to achieve the desired security level.

Prover Architecture

zkMIPS's prover architecture employs a multi-stage proof composition strategy to achieve scalable zero-knowledge computation. The system combines novel constraint reduction techniques with optimized polynomial commitment schemes and constraint construction schemes, delivering 10x faster proving speeds compared to previous ZKM, and outperforming other zkVM implementations to date.

Core Components

The zkMIPS proving system implements a hierarchical verification model through four key components.

• Runtime Executor

  Processes program instructions, partitions execution into verifiable shards, and generates cryptographic execution records:

  • Instruction-level parallelism through pipelined execution for different shards.
  • Multiset hashing based memory state transitions.
  • Event-based constraint generation.

• Machine Prover

  Generates STARK proofs for individual execution shards using:

  • STARK config with KoalaBear field optimization.
  • Merkle Matrix Commitment Scheme (MMCS) with Poseidon2 hash algorithm.
  • FRI-based low-degree proofs.

• STARK Aggregation

  Recursively composes proofs across execution shards with custom recursive constraint chip over KoalaBear field.

• STARK-to-SNARK Adapter

  Converts aggregation proof to Ethereum-compatible format with:

  • BN254 field adaptation, compressing the STARK verifying circuit using Groth16-friendly field expression.
  • Groth16 circuit wrapping.

The final output is a ​Groth16 proof with corresponding verification key, compatible with Ethereum's Layer 1 verification infrastructure.

STARK Aggregation

zkMIPS's STARK aggregation system decomposes complex program proofs into parallelizable shard proofs and recursively compresses them into a single STARK proof.

Shard Proof Generation

zkMIPS processes execution trace proofs for shards through three key phases:

• ​Execution Shard

  Splits program execution (compiled ELF binaries) into fixed-size batches and maintains execution context continuity across shards.

• ​Trace Generation​​

  Converts each shard's execution into constrained polynomial traces and encodes register states, memory operations, and instruction flows.

• Shard ​Proof

  Generates STARK proofs for each shard independently using FRI with Merkle tree-based polynomial commitments.

The proving pipeline coordinates multiple parallel proving units to process shards simultaneously, significantly reducing total proof generation time compared to linear processing.

Recursive Aggregation

Recursive aggregations are used to recursively compress multiple shard proofs into one. The aggregation system processes verification artifacts through:

• ​Proof Normalization​​

  Converts shard proofs into recursive-friendly format.

• ​Context Bridging​​

  Maintains execution state continuity between shards.

• ​Batch Optimization​​

  Groups proofs for optimal parallel processing.

The aggregation engine implements a multi-phase composition:

• Base Layer​​

  Processes raw shard proofs through initial verification circuits and generates first-layer aggregation certificates.

• ​Intermediate Layers​​

  Recursively combines certificates "2-to-1" using recursive-circuit.

• ​Final Compression​​

  Produces single STARK proof through final composition step.

STARK to SNARK

zkMIPS's STARK-to-SNARK proof recursion enables efficient on-chain verification by transforming STARK proofs into SNARK-compatible formats through a two-stage cryptographic transformation pipeline. This process reduces proof size​ while achieving constant-time verification \(O(1)\) independent of circuit complexity.

Field Adaptation and Circuit Shrinkage

This stage transforms proofs from STARK's native field (quartic extension field over KoalaBear Prime) to BN254-friendly format through:

• ​Proof Compression:

  Reduces proof length via a recursive compression method.

• Recursive Field Conversion:

  Transforms proofs from STARK's native field (quartic extension field over KoalaBear Prime) to BN254-friendly format.

SNARK Wrapping

This stage finalizes SNARK compatibility through:

• ​Circuit Specialization

  Generates Groth16-specific constraint system.

• ​Proof Packaging

  Encodes proofs using BN254 elliptic curve primitives.

• ​On-Chain Optimization

  Implements optimized on-chain pairing verification.

Proof Composition

zkMIPS enables developers to implement recursive proof verification through its innovative proof composition system, allowing cryptographic proofs to be nested within zkVM programs. This architecture supports aggregation of multiple proofs while maintaining compatibility with zkMIPS's verification framework.

Key Use Cases

Proof composition enables developers to verify existing proofs within new ones.Typical use cases include:

• Privacy-Preserving Computation

  • Confidential Data Processing

    Execute distributed computations on private data pieces while generating unified proofs.

  • ​Cryptographic Proofs

    Verify encrypted values without decryption (e.g., zero-knowledge encryption proofs, digital signatures, homomorphic encryption).

• Proof Aggregation

  • Cross-chain Verification

    Combine proofs from multiple chains into one (e.g., Ethereum).

  • ​Rollup Optimization

    Compress numerous transaction proofs into a single batch proof.

• Modular Program Architecture

  • Maintainability

    Update modules without recomputing entire workflow.

  • Pipeline Proof/Verification

    Split computational tasks into independent sub-proofs and execute them concurrently to optimize proving efficiency.

Core Components

zkMIPS's proofs are packaged into an object called a receipt. Composition allows users to verify a receipt inside a zkVM program. The result is a proof that a given receipt was verified. Key components include:

• Assumption

  Describes an assertion requiring proof verification.

• Receipt Claim

  Receipt statement, used to identify the receipt, containing program image ID and public inputs/outputs (SHA-256 commitment).

• Inner Receipt

  Base proof container, including STARK proof, public values and receipt claim.

• Assumption Receipt

  Conditional proof with pending dependencies on other claims.

• Composite Receipt

  Recursively verified proof bundle containing multiple verification layers.

• Final Recipt

  Final verification artifact with all assumptions resolved.

Implementation Workflow

Proof Generation Process

• Base Proof Generation

  Generates STARK proof for nested guest program, derives initial inner receipt.

• Recursive Composition

  Recursive STARK aggregation of the main program, using inner/composite receipts as inputs.

• Final Receipt

  Combine all inner receipts and composite receipts.

Verification Process

• Validate main proof's STARK constraints (composite receipt verification).
• Recursively verify all assumption proofs (inner receipt validation).
• Check SHA-256 commitment consistency across all receipt claims.

Continuation

zkMIPS implements an advanced continuation framework within its zkVM architecture, combining recursive proof composition with ​multi-shard execution capabilities. This design enables unbounded computational scalability with cryptographically verifiable state transitions while minimizing resource overhead. It has the following advantages:

• Scalability ​ Shards avoid single proof size explosion for long computations.

• Parallelism

  Independent shard proving enables distributed proof generation.

• ​State Continuity

  Overall memory consistency checking and consecutive program counter verifying ensures protocol-level execution integrity beyond individual shards.

Session-Shard Structure

A program execution forms a ​Session, which is dynamically partitioned into atomic ​shards based on cycle consumption. Each shard operates as an independent local execution with its own proof/receipt, while maintaining global consistency through cryptographic state binding.

Key Constraints

• Shard Validity

  Each shard's proof must be independently verifiable.

• Initial State Consistency

  First shard's start state must match verifier-specific program constraints (i.e., code integrity and entry conditions).

• Inter-Shard Transition

  Subsequent shards must begin at the previous shard's terminal state.

Proof Overflow

• Shard Execution Environment

  Shards operate with isolated execution contexts defined by:

  • ​Initial Memory Image: Compressed memory snapshots with Merkle root verification.
  • Register File State: Including starting PC value and memory image.

• Shard Proof

  Prove all instructions' execution in this shard, collecting all reading memory and writing memory records.

• Session Proof Aggregation

  Global session validity requires ​sequential consistency proof chaining:

  • Overall memory consistency checking.
  • Program counters consistency checking.
  • Combine shard proofs via folding scheme.

References