Lookup Arguments
Lookup arguments allow generating cryptographic proofs showing that elements from a witness vector belong to a predefined table (public or private). Given:
- Table \(T = \{t_i\}\), where \(i=0,…,N−1 \) (public/private)
- Lookups \(F = \{f_j\}\), where \(j=0,…,M−1 \) (private witness)
The protocol proves \(F \subseteq T \), ensuring all witness values adhere to permissible table entries.
Since its inception, lookup protocols have evolved through continuous optimizations. Ziren implements the LogUp protocol to enable efficient proof generation.
LogUp
LogUp employs logarithmic derivatives for linear-complexity verification. For a randomly chosen challenge \(\alpha\), the relation \(F \subseteq T\) holds with high probability when: \[ \sum_{i=0}^{M-1} \frac{1}{f_i - \alpha} = \sum_{i=0}^{N-1} \frac{m_i}{t_i - \alpha} \] , where \(m_i\) denotes the multiplicity of \(t_i\) in \(F\). See full protocol details.
LogUp Implementation in Ziren
Cross-chip verification in Ziren utilizes LogUp for consistency checks, as shown in the dependency diagram:
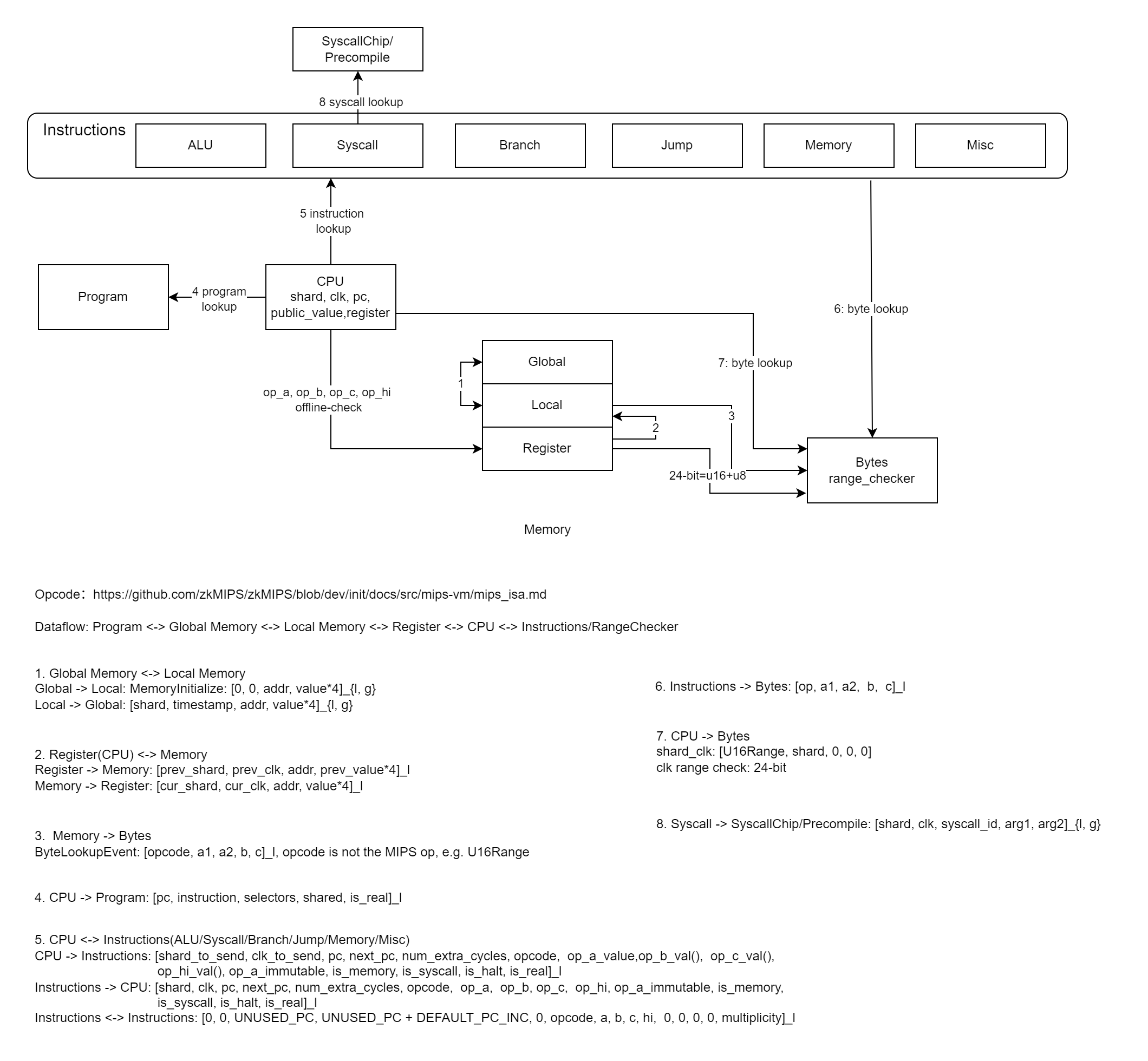
Key Lookup Relationships:
| Index | Source(F) | Target(T) | Verification Purpose |
|---|---|---|---|
| 1 | Global Memory | Local Memory | Overall memory consistency * |
| 2 | CPU | Memory | Memory access patterns |
| 3 | Memory | Bytes | 8-bit range constraints |
| 4 | CPU | Program | Instruction validity |
| 5 | CPU | Instructions | Instructions operations |
| 6 | Instructions | Bytes | Operand bytes verification |
| 7 | CPU | Bytes | Operand range verification |
| 8 | Syscall | Precompiles | Syscall/precompiled function execution |
* In the latest implementation, Ziren employs multiset-hashing to ensure memory consistency checking, enhancing proof efficiency and modularity.
Range Check Implementation Example
8-bit Range Check Design
In Ziren's architecture, 32-bit values undergo byte-wise decomposition into four 8-bit components, with each byte occupying a dedicated memory column. This structural approach enables native support for 8-bit range constraints (0 ≤ value < 255) during critical operations including arithmetic logic unit (ALU) computations and memory address verification.
- Starting Lookup Table (T)
| t |
|---|
| 0 |
| 1 |
| ... |
| 255 |
For lookups \(\{f_0, f_1, \dots, f_{M-1}\}\) (all elements in [0, 255]), we:
- Choose random \(\alpha\);
- Construct two verification tables.
-
Lookups (F)
f \(d = 1/(f-\alpha)\) sum \(f_0\) \(d_0=1/(f_0-\alpha)\) \(d_0\) \(f_1\) \(d_1=1/(f_1-\alpha)\) \(d_0 + d_1\) \(f_2\) \(d_2=1/(f_2-\alpha)\) \(d_0+d_1+d_2\) ... ... ... \(f_{M-1}\) \(d_m=1/(f_{M-1}-\alpha)\) \(\sum_{i=0}^{M-1}d_i\) -
Updated Lookup Table
t m \(d = m/(f+\alpha)\) sum 0 \(m_0\) \(d_0 = m_0/\alpha \) \(d_0\) 1 \(m_1\) \(d_1 = m_1/(1-\alpha)\) \(d_0 + d_1\) 2 \(m_2\) \(d_2 = m_2/(2-\alpha)\) \(d_0+d_1+d_2\) ... ... ... .. 255 \(m_{255}\) \(d_{255} = m_{255}/(255-\alpha)\) \(\sum_{i=0}^{255}d_i\)
,where \(m_i\) denotes the occurrence count of \(i\) in lookups.
LogUp ensures that if the final cumulative sums in both tables match (which is exactly \[ \sum_{i=0}^{M-1} \frac{1}{f_i - \alpha} = \sum_{i=0}^{N-1} \frac{m_i}{t_i - \alpha} \] ), then with high probability every \(f_i\) originates from table \(T\) (i.e., falls within 0-255 range).